《每周工作 4 小时》读书笔记 - 寻找生活工作的平衡
怎么知道的这一本书
我已经忘记了最初是因为什么原因把这一本书添加到了书单中了,但是看了一下同期加入书单的图书,还有 [[毫无意义的工作]],可能是不知道从哪边看了一篇关于工作生活的文章,里面可能提到了这一本书,就这个名字就像让人把它加入待看列表。最近在 Twitter 有一个关键词 [[Indie Hacker]] 又再一次被频繁提起,与之关联的 [[Digital Nomad]],独立开发者,[[Company of One 一人公司]]等等,都成为了最近的流行趋势。在 OpenAI,Bard,[[Claude]] 等等 AI 辅助工具的帮助情况下,个人可以找到方式将自己从朝九晚五的工作中解放出来。
无独有偶的是昨天晚上刚刚听到一个播客,这个播客是讲跨境电商的从业人员如何借助 OpenAI,[[Midjourney]] 的能力,将自己的效率提升了 4 倍,原来需要在一天时间内做的事情,可以很快在一个上午,几小时之内完成,之前一个礼拜的工作可以很快在一天时间内完成。而这也恰恰是本书作者 [[蒂莫西 费里斯]] 想要在书中所倡导的,「工作的关键是高效,而不是忙碌」。令我更惊讶的是,本书出版于 2012 年,但他所倡导的理念却在近 10 年之后才慢慢被人所接受。
关于作者
作者 Timothy Ferriss(蒂莫西·费里斯) ,我虽然第一次看到这个名字,但是在读完简单的查询了之下之后,我就发现了另一个我经常见的名字 Tim Ferriss,有一档播客叫做 The Tim Ferriss Show,一下子就对这个作者熟悉来起来,也瞬间知道了为什么他能够这么早就能这样思考生活和工作的关系。
几句话总结书的内容
《每周工作 4 小时》是由蒂莫西·费里斯撰写的一本畅销励志书。在书中探讨了如何通过优化时间和工作流程,实现更高效的工作和更丰富的生活。作者提出了一种颠覆传统工作模式的思维方式 —- 每周工作 4 小时,鼓励读者追求自由、创造性和富足的生活。
- 只做重要的事情,减少工作时间
- 少做无意义的工作
- 作者强调了时间管理的重要性,推崇使用“帕累托法则”来提高工作效率。他鼓励读者学会集中注意力,避免无意义的忙碌,并通过列出优先事项和设定时间限制来实现高效工作。
- 自动化或外包工作
- 提倡通过自动化和外包来减轻工作负担。建议将一些重复、低效的任务交给他人处理或自动化处理,从而腾出更多时间和精力投入到更有价值的事务上。
- 无固定办公地点、远程办公
- 鼓励读者采取远程办公或灵活工作时间的方式,摆脱传统的朝九晚五的工作模式。他认为,随着科技的进步,人们可以利用互联网和通信工具,在任何地方都能进行工作,从而实现更自由的生活方式。
- 追求兴趣和激情
- 强调了追求兴趣和激情的重要性。他鼓励读者寻找自己真正感兴趣的事物,并将其转化为收入来源,从而实现工作与生活的平衡。
Tim Ferriss 在书中所倡导的思想,和 FIRE 理念 所倡导的思想非常相似,Tim Ferriss 则更关注于时间管理和有效工作,倡导[[迷你退休]],将退休生活拆分到日常生活中。而 FIRE 运动的理念则更强调通过控制支出,增加收入,累积财富,给退休设定了一个「标准」。而这两种「思考」的方式殊途同归,我们的终极目标并不是放弃工作去旅行,去放纵,而是为自己争取一些自由的时间和空间,让我们可以在世界的任何地方都可以享受自我。这两种思想可以相互补充,他们即不矛盾,也不相互排斥。
大部分人,包括过去的我,总是试图尽力说服自己相信生活本就是如此。用朝九晚五的劳作去换取短暂的周末或极为短暂的假期,还要冒着随时可能被解雇的风险。
千万不要做的 9 件事情
- 不接不熟悉的电话
- 别把收发邮件当成早上的第一件事
- 不要在没有详细日程表或结束时间的情况下去参加会议或接听某个电话
- 别给人闲扯的机会
- 不要连续查看邮件,只应该在固定时间段查看
- 不要和低效能高维护成本的顾客过度沟通
- 不要靠加班来解决过剩的工作,要有优先级
- 不要 24 小时带着手机或电脑
- 不要期待工作能够填补非工作关系或工作之外的活动能带给你的那些东西
11 个信条提高利润
- 恰当的定位(目标市场)
- 制定市场战略的时候,向大众描述产品
- 可度量的事情,才是可以驾驭的
- 度量学的原理很有价值。统计一起可以度量的数据,运营统计,投入产出比,计算广告,完成度,期望收益,付款人拒付,坏帐等,回报率等等
- 定价优先于产品,先找好销售渠道
- 少即是多,减少中间环节以扩大利润
- 创造需求而不是提供措施
- 广告只在第一次做时有用,好形象通常是多余的
- 降低负面,保障正面。牺牲掉边际贡献,以确保投资安全
- 不要急于谈判,应先让对手跟自己讨价还价
- 高活跃度 VS 产出率—- 80/20 法则和帕雷托定律
- 所期待的 80% 的效果来自 20% 的努力
- 顾客并不总是对的—-「解雇」难缠的客户
- 截止日期甚于细节 —- 先测试可信赖性,再测试能力
总结
虽然书中有一些具体的建议,如今来看已经过时,比如作者推荐的 Evernote,就刚刚出现被并购,并裁去了所有员工的新闻,但是作者想要表达的思想却是对的,那就是 Evernote 可以让我们可以在一个地方查询到所有的信息,不管是在网页上看到的,还是自己记录的,还是发表的内容,合同的内容,通过 OCR 识别,都可以被找到。虽然 Evernote 看起来不行了,但是还存在很多其他的工具可以让我们去使用。
作者在书中所倡导的工作方式,引发了对传统工作模式的反思,并且以个人案例和经验提供了实用建议和技巧,让读者更好地管理时间、提高工作效率,并追求更自由和富足的生活。
启发或想法
忙碌的人忙于任何事情,除了生活
作者通过思考工作和生活,提出了一个引人深思的问题,「我们必须要在每周的工作上花费 40 小时吗?」,显然答案是否定的,「先成为企业家,再成为雇员」囊括了作者核心思想。在过去的全球化发展过程中,尤其是互联网的发展将全世界拉到了一起,可以利用互联网将产品直接销售给客户,从而实现被动收入,通过创造的方式来建立自己的品牌和资产,通过自动化或外包的形式将不重要的或不想做的事情分包出去,从而提高自己的效率。而在具体的工作中,作者也提供了具体的细节行动,比如区分优先级,使用 80/20 法则选择客户来缩短工作时间。
谁应该看这本书
- 疲惫于每周 40 个小时的工作的人
- 渴望从事远程工作,希望过上数字游民([[Digital Nomad]])生活的人
印象深刻的句子
- 重新定义一下「懒惰」,懒惰是容忍令人不满的现状,让客观环境或其他人决定自己的生活。
- 良性压力(enstress),英文中 eu- 前缀,在希腊语中是「有益的、良好的」意思。激励我们超越自我的行为榜样,消除腰部赘肉的体育训练,拓展我们适应范畴的冒险都是良性压力。有益健康,能促进我们成长。
- 并非所有的顾客都生而平等。
- 关键是高效,而不是忙碌
- 刻意安排的时间永远都不准确
- 不欢迎任何批评的人必定会失败。我们需要避免的是那种毁灭性的批评,而不是所有的批评。
开源的数据分析工具 Metabase
Metabase 是一个开源的商业数据分析(Business Intelligence,缩写 BI)工具。Metabase 可以将数据库中的数据以各种图表的方式展示出来,分析师只需要通过简单的查询语句就可以通过 Dashboard 展示出来。Metabase 提供一个直观易用的用户界面,非技术人员也能够轻松地进行数据分析和可视化。它支持多种类型的数据库,包括 MySQL、PostgreSQL、Oracle 等,并提供了一些预定义的查询和报告模板,帮助用户快速开始分析工作。
什么是 BI
BI 是 Business Intelligence 的缩写,代表的是一种通用商业分析的解决方案,即:用一系列技术手段对数据加工和分析,转化为知识进而支持商业决策的系统。
BI 的范围需要涵盖大量工具,包括数据源连接、数据准备、数据可视化、数据报表、数据输出等。常见的 BI 工具有:Microsoft Power BI、Tableau 等,国内有 阿里云 Quick BI、FineBI 等。开源方案,包括 [[Superset]]、Hue、[[Redash]]、以及本文介绍的重点 Metabase 等。
Metabase
Metabase 的主要特点包括:
- 数据可视化:Metabase 提供了各种图表类型,如柱状图、折线图、饼图等,使用户能够以直观的方式展示数据,并通过交互式控件进行数据筛选和过滤。
- 支持的图表类型包括:折线图、柱状图、饼图、面积图、组合图、地图、漏斗、散点、仪表盘等
- 支持的数据源:Postgres、MySQL、Druid、SQL Server、Redshift、MongoDB、Google BigQuery、SQLite、H2、Oracle、Vertica、Presto、Snowflake、SparkSQL。
- 邮件报警:可以使用已有查询配置数据阈值报警,发送邮件。
- 查询构建器:Metabase 提供了一个简单而强大的查询构建器,用户可以通过拖放方式选择字段和条件来构建查询语句,无需编写复杂的 SQL 语句。
- Dashboard:Metabase 允许用户创建仪表板(Dashboard),将多个图表组合在一起展示,并支持自定义布局和样式。
- 数据分享:用户可以将他们创建的报表和仪表板分享给其他人,在权限控制的基础上共享数据分析结果。
- 内置问题库:Metabase 内置了一个问题库(Question),为常见问题提供了标准化答案模板,帮助用户快速回答常见问题。
- 自动化报告:Metabase 可以根据用户设定的时间表,自动执行查询和生成报告,方便用户定期获取数据分析结果。
- 仪表板功能:支持参数传递、一键全屏、公开分享、iframe 嵌入、定时刷新
- 用户集成:LDAP、OAuth2(需做一点开发)
- 权限:支持按数据源或者报表文件夹分配权限给用户组。
安装 Metabase
简单使用 Docker 安装
version: '3'
services:
metabase:
image: metabase/metabase:latest
container_name: metabase
restart: always
ports:
- ${PORT:-3000}:3000
environment:
- MB_JAVA_TIMEZONE=${MB_JAVA_TIMEZONE:-Asia/Shanghai}
通过 Docker 运行 Metabase,将其映射到本地 3000 端口。然后可以通过浏览器访问 http://localhost:3000 来打开 Metabase 的用户界面。
首次访问时,会要求设置管理员账号和密码。设置完成后,就可以开始使用 Metabase 了。Metabase 提供了一个直观的用户界面,首先需要关联数据源,然后就可以轻松地查询数据库中的数据,并将其以各种图表的方式展示出来。用户可以通过提问(Question)功能来创建查询,然后将查询结果保存为仪表盘(Dashboard)。
Metabase 使用
Metabase 的使用主要是分成如下步骤:
- 创建数据源
- 创建查询语句
- 简单查询,简单的数据,可以界面操作完成直接展示数据
- 自定义查询,过滤条件和查询条件
- 原生查询,直接使用 SQL 语句查询
如果在初始化的时候没有设置自己的数据源,那么也可以在 Admin 页面中添加数据源。
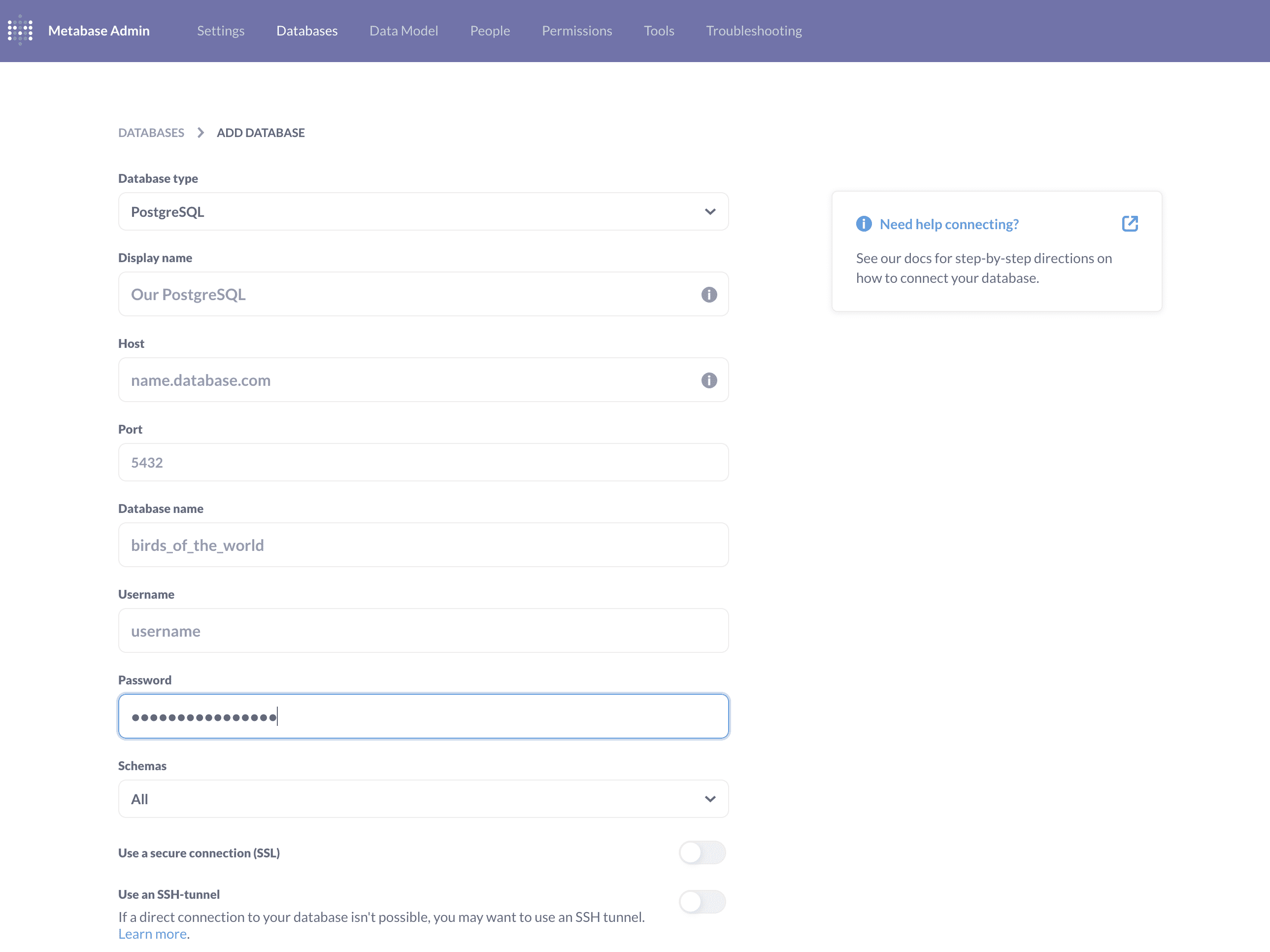
reference
- https://t.co/EDIHgxiH0I
使用 k6 做一次负载性能测试
负载测试(性能测试,压力测试)是一个较为复杂的任务,包括了测试目标,工具开发,脚本开发,CI 集成,结果分析,性能调优等等部分,可以衡量服务是否是一个高可用,高性能的服务。负载测试能检验在不同的工作负荷下,服务的硬件消耗和响应,从而得到不同负载情况下的性能指标。压力测试能检验软硬件环境下服务所能承受的最大负荷并帮助找出系统瓶颈所在。
k6 是什么
k6 是用 Go 语言编写的一种高性能的负载测试工具。
k6 具有下面几个特点
- 可配置的负载生成(Configurable load generation),低配置的机器就可以生成大量流量
- 利用代码进行测试(Tests as code),重用测试脚本,模块化逻辑,版本控制,和 CI 集成
- 功能齐全的 API(A full-featured API),脚本 API 提供多种模拟真实应用程序流量的功能。
- 强大的 CLI 工具。
- 内嵌的 JavaScript 引擎(An embedded JavaScript engine),提供了 Go 的性能,和 JavaScript 脚本的熟悉度灵活度
- k6 嵌入了 JavaScript 运行时,可以使用 JavaScript ES2015/ES6 来编写脚本。
- 多种协议的支持(Multiple Protocol support),HTTP,WebSockets 和 gRPC
- 庞大的插件支持生态(Large extension ecosystem),借助 k6 来扩展需求,并且很多人通过社区分享他们的扩展
- 灵活的指标存储和可视化(Flexible metrics storage and visualization),汇总统计数据或粒度指标,导出到您选择的服务。
- 使用 Checks 和 Thresholds 可以更加轻松的做面向目标的自动化的负载测试。
为什么选择 k6
[[性能测试工具]]有很多
- [[Hey]] Hey 是一个使用 Golang 实现的 HTTP 压测工具。
- [[Apache Bench]] Apache Bench 是一个轻量的 HTTP 压力测试工具。
- [[vegeta]] vegeta 是一个开源的 HTTP 压力测试工具。
- [[Apache JMeter]],使用 Java 编写的开源的性能测试工具
- [[Tsung]] Tsung 是一个 Erlang 编写的多协议支持的测试工具。
- [[LOCUST]],LOCUST Python 编写的性能测试工具,基于代码的方式定义用户行为,支持分布式测试
- [[Gatling]],Scala 编写,使用异步,非阻塞的方式模拟用户访问,提示实时的结果和报告
- [[Siege]], Siege 是一款使用 C 语言编写的性能测试工具
- [[Artillery]],Artillery 是一个 JavsScript 编写的,基于云端的压力测试工具。
- [[Drill]],drill 是一个 [[Rust]] 编写的 HTTP 压力测试工具。
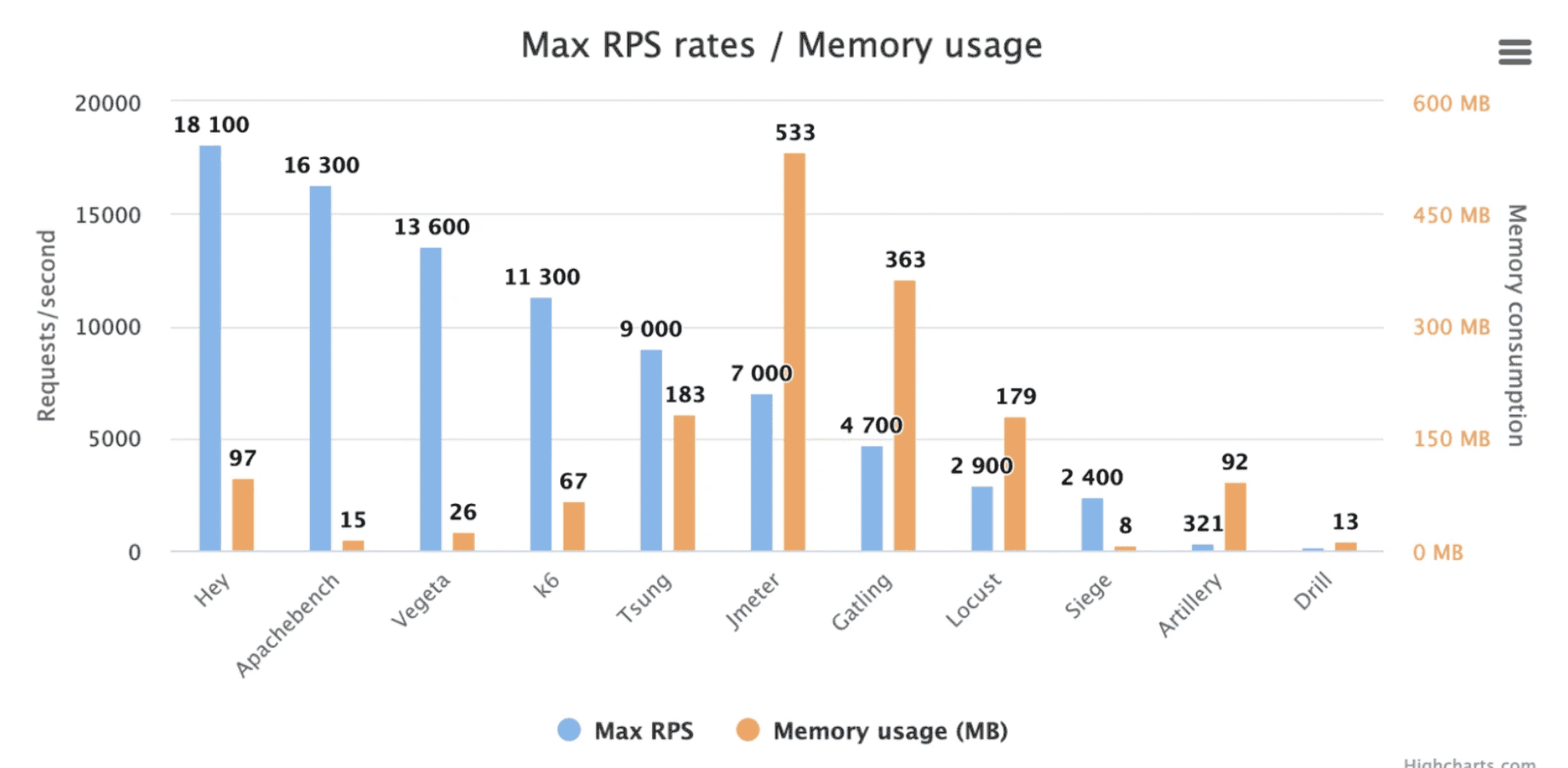
k6 的优势在于 :
- k6 支持 TypeScript 编写脚本,如果熟悉 TypeScript 学习成本比较低
- 支持 metrics 输出,可以记录到 [[InfluxDB]] 等
- 可以与多种 CI 工具集成,可以于 Grafana 进行集成展示结果数据
k6 vs JMeter
虽然 JMeter 在支持的协议数量上要优于 k6,但是 K6 相对于 JMeter 还是有不少的优势的 :
- 因为 k6 是 Go 编写的,相对于 Java 编写的 JMeter 有性能上的差距,K6 可以只用较少的资源就能达到指定数量的负载。
- 支持阈值
- TypeScript 的脚本可以更好的促进协作和版本管理
- 资源利用率远远强于 JMeter
- 丰富的可视化方案
Load-testing
测试的类型
- spike,尖峰测试,短时间内突然遭受到突发流量
- stress,压力测试,将系统置于极限负载下
- soak tests,持续性测试,连续时间内进行测试,通常是几小时或几天,这种测试旨在评估系统在长时间运行和持续负载下的稳定性,性能和资源管理能力
安装 k6
Debian/Ubuntu 可以执行如下命令1
sudo apt-get update && sudo apt-get install ca-certificates gnupg2 -y
sudo apt-key adv --keyserver hkp://keyserver.ubuntu.com:80 --recv-keys C5AD17C747E3415A3642D57D77C6C491D6AC1D69
echo "deb https://dl.k6.io/deb stable main" | sudo tee /etc/apt/sources.list.d/k6.list
sudo apt-get update
sudo apt-get install k6
Docker
docker pull loadimpact/k6
HTTP 请求
新建一个 script.js 文件
Get 请求 get(url, [params])
import http from 'k6/http';
// 默认控制选项
export let options = {
vus: 10, // 指定要同时运行的虚拟用户(VUs)数
duration: '10s', // 指定测试运行的总持续时间
};
// default 默认函数
export default function() {
// 标头
let params = { headers: { 'Content-Type': 'application/json' } };
var res=http.get("https://test.k6.io", params)
}
说明:
- VUs, virtual users, 虚拟用户,更多的虚拟用户意味着更高的并发流量
对于 options 也可以通过设置可变的形式来设置不同阶段
export const options = {
stages: [
{ duration: '30s', target: 20 },
{ duration: '1m30s', target: 10 },
{ duration: '20s', target: 0 },
],
};
Post 请求 Post( url, [body],[params])
import http from 'k6/http';
export let options = {
vus: 100,
duration: '10s',
};
// default 默认函数
export default function() {
let json = { content: 'linhui', image: 'images' };
let params = { headers: { 'Content-Type': 'application/json' } };
var res = http.post("https://host/api/feedback", JSON.stringify(json), params)
console.log(res.status);
}
del 请求 del(url,[body],[params])
import http from 'k6/http';
export let options = {
vus: 1,
duration: '10s',
};
// default 默认函数
export default function () {
let json = {id:1};
let params = { headers: { 'Content-Type': 'application/json' } };
http.del('https://host/delete', json, params);
}
batch 批处理,可以用来做页面并发,批处理并不能保证执行顺序,batch(method,url,[body],[params])
import http from 'k6/http';
export let options = {
vus: 1,
duration: '10s',
};
export default function () {
let get = {
method: 'GET',
url: 'https://host/get',
};
let get1 = {
method: 'GET',
url: 'https://host/get',
};
let post = {
method: 'POST',
url: 'https://host/post',
body: {
hello: 'world!',
},
params: {
headers: { 'Content-Type': 'application/json' },
},
};
let res = http.batch([req1, req2, req3]);
}
使用 request 发送求 request(method, url, [body], [params])
import http from 'k6/http';
export let options = {
vus: 1,
duration: '10s',
};
export default function () {
let json = { content: 'linhui', image: 'images' };
let params = { headers: { 'Content-Type': 'application/json' } };
let res = http.request('POST', 'http://host/post', JSON.stringify(json), params);
let res1 = http.request('GET', 'http://host/get', null, params);
}
执行脚本,进入脚本根目录
k6 run test.js
# 使用 docker
docker run -i loadimpact/k6 run - <test.js
常见指标说明
指标类型
| 名称 | 描述 |
| Counter | 计数器,对值进行累加 |
| Gauge | 最小值、最大值和最后一个值。 |
| Rate | 百分比 |
| Trend | 最小值、最大值、平均值和百分位数的统计数据指标 |
k6 一直都会收集的指标
| 名称 | 类型 | 描述 |
| vue | Gauge | 当前活动的虚拟用户数 |
| vue_max | Gauge | 虚拟用户的最大数量 |
| iterations | Counter | 脚本中的函数被执行的次数 |
| data_received | Counter | 接收到的数据量大小 |
| data_sent | Counter | 发送的数据量大小 |
| iteration_duration | Trend | 完成默认/主函数的一次完整迭代所花费的时间。 |
| checks | Rate | checks 项的成功率 |
HTTP 协议特有的指标
| 名称 | 类型 | 描述 |
| http_reqs | Counter | 总请求数量 |
| http_req_blocked | Trend | 在发起请求之前被阻塞的时间 |
| http_req_connecting | Trend | 建立到远程主机的TCP连接所花费的时间。 |
| http_req_tls_handshaking | Trend | 与远程主机握手建立TLS会话所花费的时间 |
| http_req_sending | Trend | 将数据发送到远程主机所花费的时间 |
| http_req_waiting | Trend | 等待远程主机响应所花费的时间 |
| http_req_receiving | Trend | 从远程主机接收响应数据所花费的时间 |
| http_req_duration | Trend | 请求的总时间。它等于http_req_sending + http_req_waiting + http_req_receiving(即,远程服务器处理请求和响应花了多长时间,而没有初始DNS查找/连接时间) |
| http_req_failed | Rate | 失败请求率 |
每一个 http 都会返回一个 HTTP Response 对象,下面是常用的一些属性。
| 属性 | 类型 |
| Response.body | HTTP 响应正文 |
| Response.cookies | 响应 cookies ,属性是 cookie 名称,值是 cookie 对象数组 |
| Response.error | 发送请求失败后的错误信息。 |
| Response.error_code | 错误码 |
| Response.headers | 标头,键值对 |
| Response.status | 从服务器收到的 HTTP 响应代码 |
| Response.timings | 耗时(以毫秒为单位) |
| Response.timings.blocked | = http_req_blocked |
| Response.timings.connecting | = http_req_connecting |
| Response.timings.tls_handshaking | = http_req_tls_handshaking |
| Response.timings.sending | = http_req_sending |
| Response.timings.waiting | = http_req_waiting |
| Response.timings.receiving | = http_req_receiving |
| Response.timings.duration | = http_req_duration |
自定义指标
import http from 'k6/http';
import { Trend } from 'k6/metrics';
export let options = {
vus: 100,
duration: '10s',
};
// 新建一个类型为 Trend 名为 sending_time 的自定制指标
let sendingTime = new Trend('sending_time');
export default function () {
let res = http.get('http://www.baidu.com');
sendingTime.add(res.timings.sending);
}
设置了 sending_time 这个自定义指标之后在 k6 运行的结果中就能看到新定义的指标。
常用 Option 选项
VUs:指定同时运行的虚拟用户数量,必须是一个整数,和 duration 搭配使用。默认值:1
export let options = {
vus: 10,
duration: '10s',
};
或者在执行命令时指定:
k6 run -u 10 test.js
k6 run --vus 10 test.js
Duration:字符串,指定测试运行的总持续时间,与 vus 选项一起使用。默认值:null
export let options = {
vus: 10,
duration: '10s',
};
执行命令时指定:
k6 run -u 10 --d 20s test.js
k6 run --vus 10 --duration 20s test.js
User Agent:发送 HTTP 请求时指定 User-Agent 标头。默认值:k6/0.27.0 (https://k6.io/) 取决于你 k6 的版本
export let options = {
userAgent: 'Mozilla/5.0',
};
k6 run --user-agent 'Mozilla/5.0' test.js
TLS Version:表示允许在与服务器交互中使用的唯一 SSL/TLS 版本的字符串,或者一个指定允许使用的“最小”和“最大”版本的对象。 默认值:null (允许所有版本)
export let options = {
tlsVersion: 'tls1.2',
};
export let options = {
tlsVersion: {
min: 'ssl3.0',
max: 'tls1.2',
},
};
TLS Cipher Suites:允许在与服务器的 SSL/TLS 交互中使用的密码套件列表。由于底层 go 实现的限制,不支持更改 TLS 1.3 的密码,并且不会执行任何操作。 默认值:null(允许所有)
export let options = {
tlsCipherSuites: [
'TLS_RSA_WITH_RC4_128_SHA',
'TLS_RSA_WITH_AES_128_GCM_SHA256',
],
};
TLS Auth: tls 身份验证。默认值:null
export let options = {
tlsAuth: [
{
domains: ['example.com'],
cert: open('mycert.pem'),
key: open('mycert-key.pem'),
},
],
};
Throw:一个布尔值,true or false ,指定是否在失败的 HTTP 请求上抛出异常。 默认值:false
export let options = {
throw: true,
};
k6 run --throw test.js
k6 run -w test.js
Thresholds:一组阈值规范,用于根据指标数据配置在何种条件下测试成功与否,测试通过或失败。默认值:null
export let options = {
thresholds: {
http_req_duration: ['avg<100', 'p(95)<200'],
'http_req_connecting{cdnAsset:true}': ['p(95)<100'],
},
};
Tags:指定应在所有指标中设置为测试范围的标签。如果在请求、检查或自定义指标上指定了同名标签,它将优先于测试范围的标签。 默认值:null
export let options = {
tags: {
name: 'value',
},
};
k6 run --tag NAME=VALUE test.js
RPS:指的是每秒发出的最大请求数。 默认值:0
export let options = {
rps: 500,
};
或者:
k6 run --rps 500 test.js
Paused:是否可以暂停和和恢复的方式运行脚本,暂停启动后需要使用另外的窗口执行k6 resume 恢复使用。在恢复窗口可以实时的查看脚本的运行情况。 启动后不支持暂停, 默认值:false
export let options = {
paused: true,
};
k6 run --paused test.js
k6 run --p test.js
No VU Connection Reuse:布尔值,是否复用 TCP 链接。默认值:false
export let options = {
noVUConnectionReuse: true,
};
run --no-vu-connection-reuse test.js
No Usage Report:布尔值,是否给 k6 发送使用报告,true 值不会发使用报告。 默认值:false
k6 run --no-usage-report test.js
No Thresholds:布尔值,是否禁用阈值。默认是:fasle
k6 run --no-thresholds test.js
No Summary:是否禁用测试结束生成的概要。默认值:false
k6 run --no-summary test.js
No Cookies Reset:是否重置 Cookies,fasle 每次迭代都会重置 Cookie ,true 会在迭代中持久化 Cookie 。默认值:false
export let options = {
noCookiesReset: true,
};
No Connection Reuse:是否禁用保持活动连接,默认值:false
export let options = {
noConnectionReuse: true,
};
k6 run --no-connection-reuse test.js
Minimum Iteration Duration:指定默认函数每次执行的最短持续时间,任何小于此值的迭代都将剩余时间内休眠,直到达到指定的最小持续时间。默认值:0
export let options = {
minIterationDuration: '10s',
};
k6 run --min-iteration-duration '1s' test.js
Max Redirects:最大重定向,默认值:10
export let options = {
maxRedirects: 10,
};
k6 run -max-redirects 10 test.js
Batch: batch 同时调用的最大连接总数,如果同时有 20 api 请求需要发出 ,batch 值是 15,那么将会立即发出 15 个请求,其余的请求会进行一个排队。默认值:20
export let options = {
batch: 15,
};
k6 run --batch 10 test.js
Batch per host:batch 对同一个主机名同时进行的最大并行连接数。默认值:6
export let options = {
batchPerHost: 5,
};
k6 run --batch-per-host 10 test.js
Blacklist IPs:黑名单。默认值:null
export let options = {
blacklistIPs: ['10.0.0.0/8'],
};
k6 run --blacklist-ip= ['10.0.0.0/8'] test.js
Block Hostnames:基于模式匹配字符串来阻止主机,如 *.example.com , 默认值:null
export let options = {
blockHostnames: ["test.k6.io" , "*.example.com"],
};
k6 run --block-hostnames="test.K6.io,*.example.com" test.js
Discard Response Bodies:是否应丢弃响应正文,将 responseType 的默认值修改成 none,建议设置成 true,可以减少内存暂用和 GC 使用,有效的较少测试机的负载。默认值:false
export let options = {
discardResponseBodies: true,
};
HTTP Debug:记录所有 HTTP 请求和响应。默认情况下排除正文,包括正文使用 –http debug=full 默认值:false
export let options = {
httpDebug: 'full',
};
k6 run --http-debug test.js
Options 的顺序
k6 提供了很多方式来设置 Options.
- CLI 选项
- 环境变量
- 脚本中的 options 对象
执行的顺序,优先级从低到高:
- Defaults,默认使用
--config- Script options
- Environment variables
- CLI Flags
如果 Options 发生冲突,那么 k6 会遵循上面的优先级,CLI flags 中的是最高优先级,会覆盖其他所有设置。
Checks 检查
Checks 类似断言,不同在于 Checks 不会停止当前的脚本。指标都可以作为检查的项目。
import http from 'k6/http';
import { sleep } from 'k6';
import { check } from 'k6';
export let options = {
vus: 100,
duration: '10s',
};
export default function () {
let res = http.get('http://test.k6.io/');
check(res, {
'状态码为200': (r) => r.status === 200,
'响应时间小于200ms': (r) => r.timings.duration < 200,
'等待远程主机响应时间小于200ms': (r) => r.timings.waiting < 200,
});
}
Thresholds 阈值
阈值是用来指定被测系统的性能预期的通过/失败标准。阈值用来分析性能指标并确定最终测试结果。内置的指标都可以作为阈值。
k6 中包含的四种度量类型每一种都提供了自己的一组可用于阈值表达式的聚合方法。
- Counter: count and rate
- Gauge:value
- Rate:rate
- Trend:p(N)
import http from 'k6/http';
import { Trend, Rate, Counter, Gauge } from 'k6/metrics';
export let GaugeContentSize = new Gauge('ContentSize');
export let TrendRTT = new Trend('RTT');
export let options = {
vus: 10,
duration: '10s',
thresholds: {
// 发出的请求数量需要大于1000
http_reqs:['count>1000'],
// 错误率应该效率 0.01%
http_req_failed: ['rate<0.01'],
// 返回的内容必须小于 4000 字节。
ContentSize: ['value<4000'],
// p(N) 其中 N 是一个介于 0.0 和 100.0 之间的数字,表示要查看的百分位值,例如p(99.99) 表示第 99.99 个百分位数。这些值的单位是毫秒。
// 90% 的请求必须在 400 毫秒内完成,95% 必须在 800 毫秒内完成,99.9% 必须在 2 秒内完成
http_req_duration: ['p(90) < 400', 'p(95) < 800', 'p(99.9) < 2000'],
// 99% 响应时间必须低于 300 毫秒,70% 响应时间必须低于 250 毫秒,
// 平均响应时间必须低于 200 毫秒,中位响应时间必须低于 150 毫秒,最小响应时间必须低于 100 毫秒
RTT: ['p(99)<300', 'p(70)<250', 'avg<200', 'med<150', 'min<100'],
},
};
export default function () {
let res = http.get('http://www.baidu.com');
TrendRTT.add(res.timings.duration);
GaugeContentSize.add(res.body.length);
}
阈值标签,测试中可以给指定的 url 或者特定标签上使用阈值。
import http from 'k6/http';
import { sleep } from 'k6';
import { Rate } from 'k6/metrics';
export let options = {
vus: 10,
duration: '10s',
thresholds: {
// type 为 baidu 使用
'http_req_duration{type:baidu}': ['p(95)<500'],
// type 为 bing 使用
'http_req_duration{type:bing}': ['p(95)<200'],
},
};
export default function () {
let res1 = http.get('https://www.baidu.com', {
tags: { type: 'baidu' },
});
let res2 = http.get('https://cn.bing.com/', {
tags: { type: 'bing' },
});
let res3 = http.batch([
[
'GET',
'https://www.baidu,com',
null,
{ tags: { type: 'baidu' } },
],
[
'GET',
'https://cn.bing.com/',
null,
{ tags: { type: 'bing' } },
],
]);
}
默认情况下没有达标阈值标准是不会停止脚本的,通过设置阈值的 abortOnFail: true 来终止。
import http from 'k6/http';
export let options = {
vus: 10,
duration: '10s',
thresholds: {
http_req_duration: [{threshold: 'p(99) < 10', abortOnFail: true}],
},
};
export default function () {
let res = http.get('http://www.baidu.com');
}
对通过的阈值前面会有一个 ✓,而失败的则会有一个 ✗ 。只有满足所有阈值的情况下测试才算通过。
日志输出
输出到控制台。
import http from 'k6/http';
export let options = {
vus: 10,
duration: '2s',
};
export default function () {
let res = http.get('http://www.baidu.com');
console.log('log')
console.info('info');
console.error('err');
console.debug('debug')
console.warn('warn')
}
输出到文件,输出到文件的同时控制台不在输出。
k6 run test.js --console-output=test.log
InfluxDB Grafana 可视化测试结果
Docker 启动 [[InfluxDB]]
docker pull tutum/influxdb
# 8083是 influxdb 的 web 管理工具端口,8086 是 influxdb 的 HTTP API 端口
docker run -d -p 8083:8083 -p8086:8086 --expose 8090 --expose 8099 --name influxsrv tutum/influxdb
Docker 启动 Grafana,
docker pull grafana/grafana
docker run -d -p 3000:3000 grafana/grafana
新建一个 k6test 数据库,访问 “http://xxxxx:8083” InfluxDB web 管理页面,新建一个 K6test 数据库

配置 Grafana 数据源
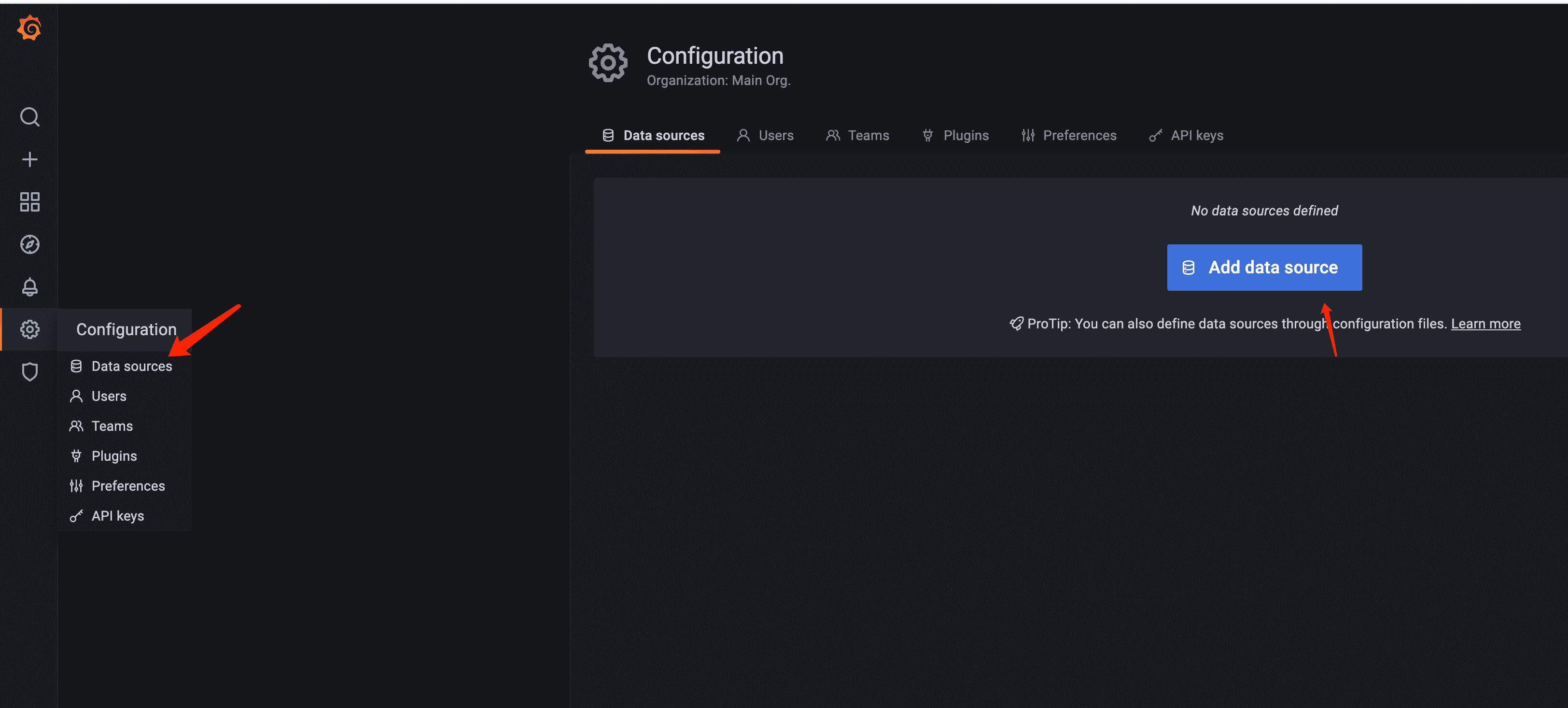
选择 InfluxDB, 填写域名端口和数据库,点击 sava&test 。出现 Data source is working 表示成功,如遇到问题查看一下端口是否放行。
导入仪表盘
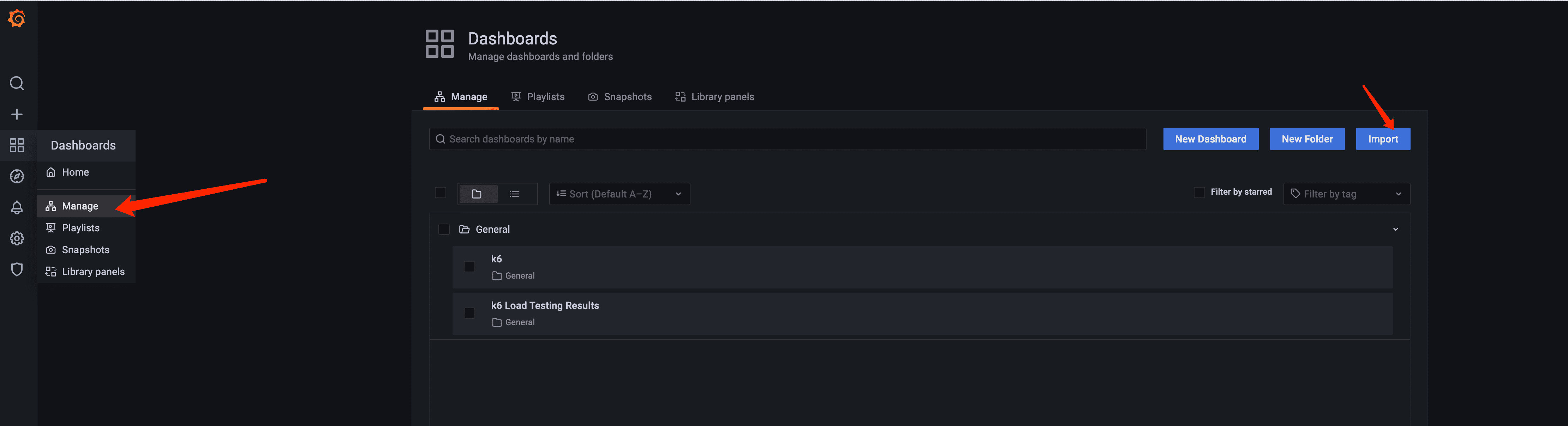
通过 ID 导入,输入 2587 点击 load 数据源选择 InfluxDB 点击 Import
官方还有几款仪表盘
将 k6 的测试指标导入到 InfluxDB
k6 run --out influxdb=http://xxxxx:8086/K6test test.js
效果图
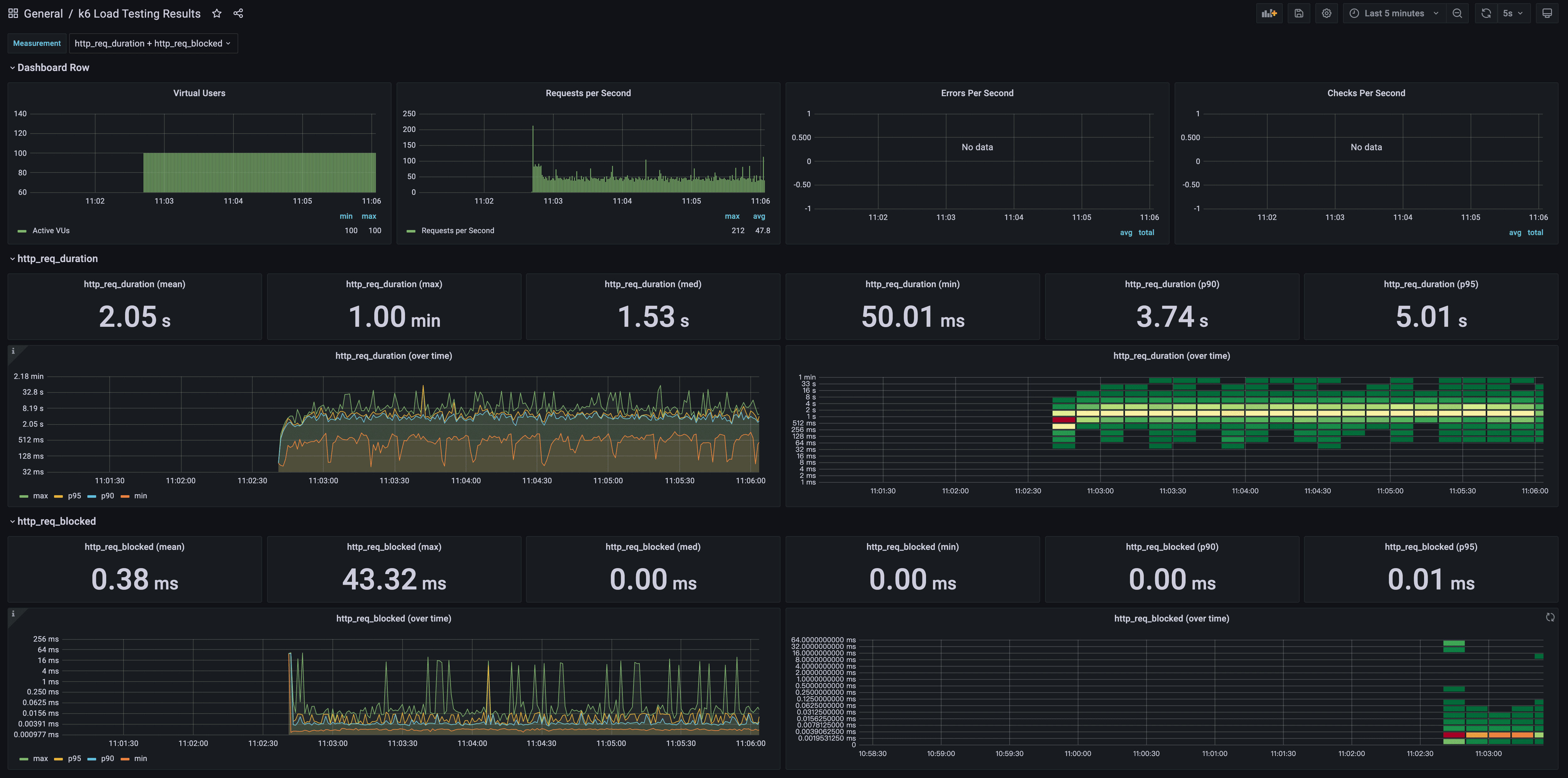
Scenarios
Scenarios (场景)配置 VU 和迭代计划的方式,通过 Scenarios 配置,可以在负载测试中对不同的工作负载或流量模式进行建模。
使用场景的优势 :
- 同一个脚本中可以声明多个场景,每个场景都可以执行不同的 JavaScript 函数
- 模拟更真实的流量,每个场景都可以使用不同的 VU 和调度模式
- 并行或顺序执行测试
- 每个场景都可以设置不同的环境变量和指标
export const options = {
scenarios: {
example_scenario: {
// name of the executor to use
executor: 'shared-iterations',
// common scenario configuration
startTime: '10s',
gracefulStop: '5s',
env: { EXAMPLEVAR: 'testing' },
tags: { example_tag: 'testing' },
// executor-specific configuration
vus: 10,
iterations: 200,
maxDuration: '10s',
},
another_scenario: {
/*...*/
},
},
};
executor 场景必须使用预定义的 executor 来配置,设置运行的时间,流量是否保持恒定,工作负载是按 VU 还是按到达率。
- 按迭代次数
shared-iterations在 VUs 之前 shares iterations,在所有并发的 VUs 中共享迭代,当所有的迭代完成时,测试结束per-vu-iterations让每一个 VU 运行配置的迭代,每个 VU 执行一定数量的迭代。
- 按 VU 数量
constant-VUs恒定数量发送 VU,在指定的时间内以恒定的并发虚拟用户数 (VUs) 执行ramping-vus根据配置阶段性增加 VU 数量,缓慢增加并发用户数
- 按 iteration rate
constant-arrival-rate以恒定速率开始迭代,ramping-arrival-rate根据配置的阶段提高 iteration rate
Scenario example
import http from "k6/http";
export const options = {
scenarios: {
shared_iter_scenario: {
executor: "shared-iterations",
vus: 10,
iterations: 100,
startTime: "0s",
},
per_vu_scenario: {
executor: "per-vu-iterations",
vus: 10,
iterations: 10,
startTime: "10s",
},
},
};
export default function () {
http.get("https://test.k6.io/");
}
shared_iter_scenario10 个 VU 进行 100 次迭代per-vu-iterations在 10 秒之后开始,10 个 VU 每个运行 10 次迭代
总结
k6 是一个非常强大的性能测试工具,只需要稍微了解一下 TypeScript,熟悉一下调用过程,就可以很快上手使用。
reference
修复 Ledger Nano X 转轴松垮问题
之前有写过一篇文章说我买了一个Ledger Nano S Plus ,整体来看 Nano S Plus 没有蓝牙功能,机身塑料质感非常强,后来看到 Nano X 打折,价格基本上已经快接近 Nano S Plus 的价格了,所以就又下单了一个 Nano X。但是没想到收货之后,发现其塑料质感和做工更加不行,并且我到货的 X,转轴部分非常松垮,只要稍微侧着拿起外面的部分,中间的机身就会溜出来。

后来简单的查了一下之后才发现原来这是 Nano X 的通病,很多人都遇到了和我一样的问题,没想到的是 100 多美元的东西做工质量这么差。但是好在这个问题可以手动进行修复。
查了之后才发现原来 Nano X 的机身和外部的铁质的外壳是可以分离的,不像 Nano S Plus 的那样是一体的。将 Nano X 的外壳铁质部分分离之后,可以将铁质部分用手或者工具稍微向内弯曲一下。力度不要太大,只需要有一个合理的弯度,可以正好卡住机身的转轴即可。
当弯曲合适之后,再将机身放入到外壳部分卡住。测试一下摩擦是否合适,如果还是太松,就重复上面的动作,直到一个合适的贴合度。
Tana 使用体验
Tana 又是一款 All-in-one 的笔记软件。我虽然很早就已经拿到了 Tana 的使用体验,但是初次体验之后因为其只提供了在线版本,无法离线使用,很快就放弃了。还是坚守在 [[Obsidian]] ,在桌面版上,随着插件的不断丰富已经成为了我常驻应用了,代替了我之前的所有笔记软件,代替了 Read it later 应用,代替了我的 WordPress 编辑器,代替了我 Jekyll 的编辑器,还代替了我用了很久的 Trello,并且我发现本地的看板完全可以代替需要网络 Loading 才能使用的 Trello。
但这一次再次想起了 Tana 是因为我又看到有人提起了 Supertags 的概念,这是一个陌生的概念。
Tana 的特性
- 没有文件夹概念
- Supertags
- 搜索 (Live query)
- 多人协作
- 唯一链接(用于分享)
消除了笔记的边界
在初次体验 Tana 的时候,最初的印象就是 Tana 的设计,所有的笔记都是通过当天的笔记开始,每一个笔记都是一个「节点」。节点之间可以相互引用,嵌套。
在 Tana 中已经完全没有了传统笔记的文件夹,文件(文档)的概念,最顶层的组织结构 Tana 称之为 Workspaces,在 Workspaces 下所有的笔记都只有节点的概念,它们可以并列,嵌套,以任意的组织形式存在。
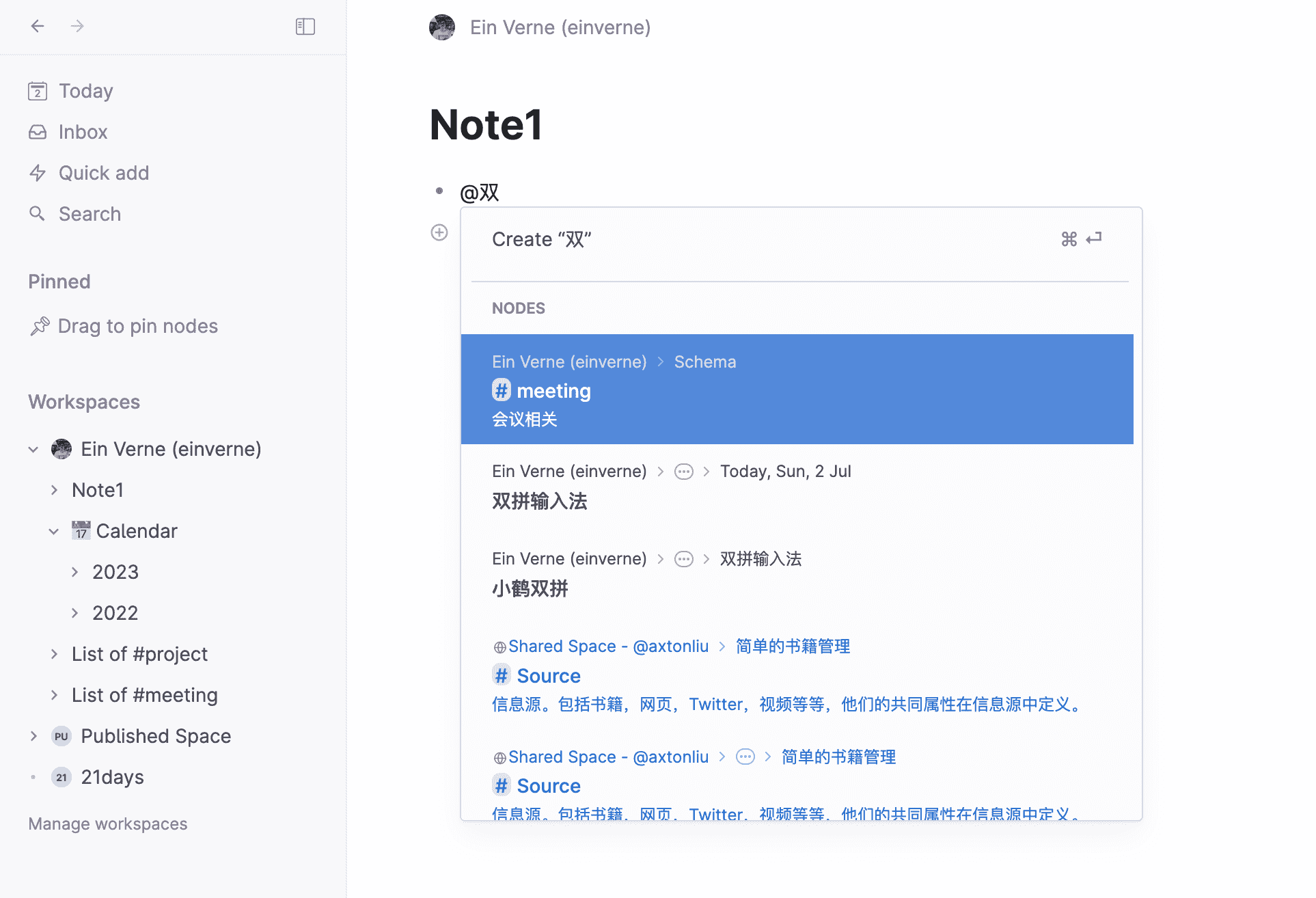
什么是 Supertags
对于普通的 Tag,我们都非常熟悉,不论是文章,还是帖子,还是 Twitter,我们都可以用 #tag 这样的方式来对文章内容进行贴标签。通过标签我们可以很快的定位这个文章、这个帖子是什么样的内容,而搜索引擎或者推荐系统也可以很快速的识别这个内容的分类。同样的浏览者也可以通过标签来找到更多的相似的内容。
而 Tana 定义的 Supertags 就是给普通的标签(tag)加上了元数据(metadata)。在 [[Obsidian]] 中普通笔记最基本的描述信息就是标签,Obsidian 也提供了方法让笔记通过标签的形式组织和检索,但是 Obsidian 中 Tag 就是最小的单位了。
为什么需要 Supertags
相信说到上面,很多就有疑问了,既然已经有了传统的 Tag,为什么还需要一个新概念 Supertags? 在上文中我提到在 Tana 中已经模糊了笔记的边界,所有节点都是一条笔记,笔记和笔记之前没有了明显的边界,那么如何在一个庞大的节点库中对这些内容进行组织就成为了棘手的问题,通过搜索?显然不够迅速,通过传统的标签,最后就会像 Obsidian 中那样还是退化成为了标签的搜索。
而 Tana 提出的解决办法就是 Supertags,比如官方的例子中,用户可以对不同节点中的内容打上 #book 的标签,并且结合 #book 和内容本身,对 book 标签进行进一步的扩充,比如 book 可以包含作者,出版时间,包含简介等等更具体的信息。在 Tana 中官方也实现了一个 AI 自动进行标签填充的功能(借助 OpenAI)。
有了这个功能之后,比如我经常在 Obsidian 中记录读书笔记的时候,常常在以书名命名的笔记前使用 YAML 定义笔记的 metadata(借助模板),而在 Tana 中我仅仅需要在节点上添加一个 #book 标签,那这个节点所需要的所有元数据都会包含在这个标签中。通过这样组织方式,节点之间会形成非常复杂的关系。
而每当用户创建一个标签,Tana 都会自动提示创建一个 List of #book 通过标签的关键,可以直接查询出所有包含这个 #book 的笔记内容,间接地将网状结构的笔记内容提取成为了一个线性的。怪不得 Tana 自己在介绍 Supertags 的时候就称 Supertags 是所有内容的 Glue。
Supertags 的继承关系
在 Tana 之中,标签是有继承关系的,我们都知道面向对象编程三大特点之一的继承目的就是为了复用代码,而在 Tana 中,通过继承(Extend)就使得标签也可以继承标签。这样就非常容易扩展标签。
比如有 #book 这样的标签,同样会有 #fiction ,#non-fiction 等等的标签,而这些具体的标签都可以继承 #book 的属性。
Supertags 能做什么
一个设计良好的 Supertags 可以让界面变成任何你想要达成的效果。
比如设计一个 #todo 标签,包含 Start Date, Due Date,Status 等属性,那么就可以轻松地创建一个类似 Trello 的看板画面。
如果像上面一样创建一个 #book 权限,添加一个属性 Status(待读,在读,已读),你就创建了一个类似豆瓣的 Track 读书记录的工具。
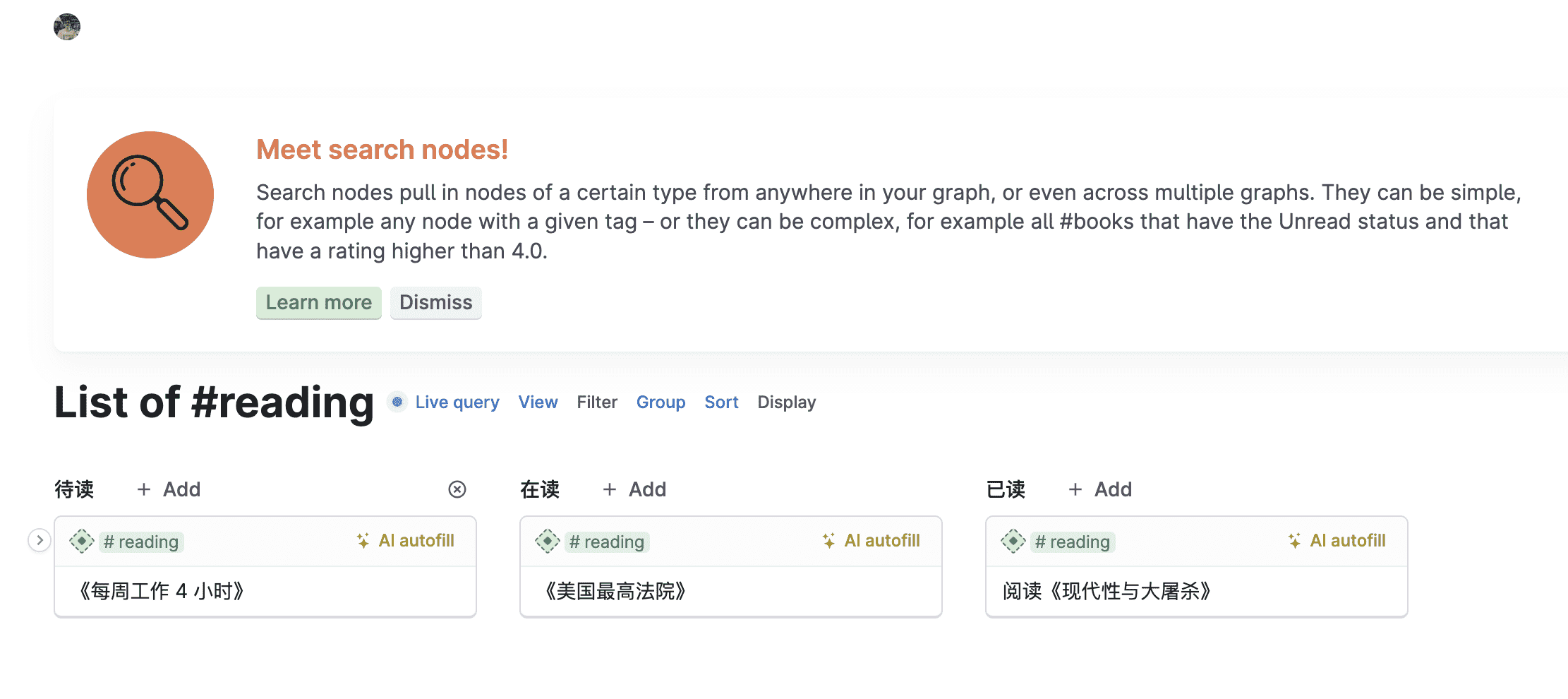
所以这就是为什么很多人说 Tana 实际上就是一个数据库的原因。只要用户发挥想想,充分利用 Tana 的展示形式(List,Table,Cards,Tabs,Calendar),以及 Filter,Group,Sort 就能展示出任何想要的界面。
获取 Tana 的测试权限
- 从官网 申请进入 waitlist
- 进入官方的 Slack 在频道中自我介绍获取
- 找拥有 Tana 邀请权限的用户
- 可以加入 Telegram Group 找我索要,
但是我只有一个邀请,先到先得,加入群组的朋友们可以相互帮助一下
- 可以加入 Telegram Group 找我索要,
总结
只有当一个工具对当前工作效率提高具有压倒性的优势时,我才会考虑替换。我过去曾经使用很多年的 [[WizNote]],积累了上千条笔记,虽然有 Evernote,OneNote 等等工具的出现,但都没有让我切换过去,直到 Obisidian 的出现,弥补了 WizNote 对 Markdown 的支持,强大的双链,非常快速的检索,以及强大的社区插件支持,让我在体验不久之后就毅然决定使用,并一直使用到现在。
我切换使用 Obsidian 的决定性原因就是 Obsidian 让我意识到了笔记不是一个摘录的工具,而是可以组织自己想法,让想法和想法之间产生关联的思考方式。并且 Obisidian 的全离线化设计让我非常放心的不会去考虑隐私等等问题。Obsidian 的开放程度也让 Obsidian 可以快速的融入任何其他的工具中,[[Anki]],[[Zotero]],[[Readwise]] 等等。
Tana 的设计思想,确实融合了很多优秀笔记的特点,但是其 Supertags 的功能,还不足以让我放弃现在的 Obsidian。所以之后还会继续观察 Tana 的发展。
不足
- 编辑器的样式不足,我之前总结的 Vim Everywhere 在这里就失效了,纯网页的操作,缺少了 Vim 快捷键的操作逊色了不少
- 不支持 Markdown
- 数据存储在云端,只支持手动导出 JSON 格式的文档
reference
macOS 下利用 Karabiner Elements 修改日本 JIS 键盘布局到美式键盘布局
JIS 键盘布局
JIS 键盘布局是日本是最常见的键盘布局,它与国内常用的美式键盘布局有一些不同之处。如果你习惯了美式键盘布局,使用 JIS 键盘可能会感到不便。
可以明显感到区别的是
- JIS 键盘的空格键非常短,我个人几乎只能使用左手大拇指来按
- 空格左边原来非常高频使用的 Command 按键变成了「英数」按键,同样空格键右侧的 Command 按键也变成了 かな
- 原来美式键盘的 Caps Locks 变成了 control 按键,虽然使用 Vim 有些人还会被鸡肋的 Caps Locks 手动修改成 Control 键,当时我一直都是将 Caps Locks 修改成按下就表示同时按下 Command + Ctrl + Option + Shift 这样的组合按键(Hyper Key),然后通过 Caps Locks 按键组合其他快捷键就可以实现非常多的功能,比如 Caps Locks + hjkl 快速调节窗口的位置,Caps Locks + f 全屏窗口等等,我都用 [[Hammerspoon]] 和 [[Karabiner Elements]] 这样的工具实现了,但是在 JIS 键盘下就把我的习惯给打破了
- 最后一个令我非常不习惯的就是数字按键 1 左边的
~按键,写 Markdown 非常常用的 tilde 按键(行内格式化代码) 在 JIS 键盘中消失了 - 最后还有一些细节部分,比如 JIS 键盘上退格键非常小!但是 Enter 键却又特别大!

通过 Karabiner Elements 修改键盘布局
Karabiner Elements 是一款强大的键盘映射工具,可以很容易地修改 JIS 键盘布局到美式键盘布局。本文将向你展示如何使用 Karabiner Elements 来实现这一目标。
首先,你需要下载并安装 Karabiner Elements。你可以在官方网站上找到适用于 macOS 的安装程序,并按照指示进行安装。一旦安装完成,你就可以打开 Karabiner Elements 并开始配置键盘映射。
或者通过 brew 来安装
brew install --cask karabiner-elements
在 Karabiner Elements 的界面中,点击左侧的“Complex Modifications”选项卡,然后点击右下角的“Add rule”按钮。在这个界面也可以通过从在线网站导入的方式。点击 Import more rules from Internet,来从网站下载更多的规则。打开网站规则列表,其中包含各种可用的键盘映射规则。
在规则列表中,找到“Japanese JIS Keyboard to US Keyboard:Remap Symbol Keys”规则,并勾选它。这将启用该规则并应用键盘映射。
接下来,你可以点击右侧的“Details”按钮,以查看该规则的详细信息。在这里,你可以看到该规则将会对哪些键进行映射,以及映射的具体内容。默认情况下,该规则将会将 JIS 键盘布局中的一些键映射为美式键盘布局中的相应键。例如,JIS 键盘布局中的 “@” 键将会映射为 “[” 键,而 “[” 键将会映射为 “]” 键。
现在,可以关闭 Karabiner Elements,并开始使用修改后的键盘布局。打开任何文本编辑器或其他应用程序,你会发现 JIS 键盘布局已经被修改为美式键盘布局。
推荐几个英语学习工具
要想学好一门语言,是一个需要长期花时间的过程,听说读写一样都不能落下。之前我也要推荐过学习英语,就应该使用英英字典(当达到一定的词汇量之后),学习英语就应该让自己的耳朵沉浸在英语发音中(可以通过听英语播客),当能够听懂大部分的内容的时候,无字幕看电影也是一种沉浸式的学习方法,到通过[[影子跟读法]] 来练习发音,完成一个语言的听说读写之后才能形成一个学习的闭环。
这篇文章抛开那些枯燥的学习方法介绍几个非常有意思的语言学习小工具。
- [[Language Reactor]] 是一个在视频上实时显示字幕的 Chrome 插件
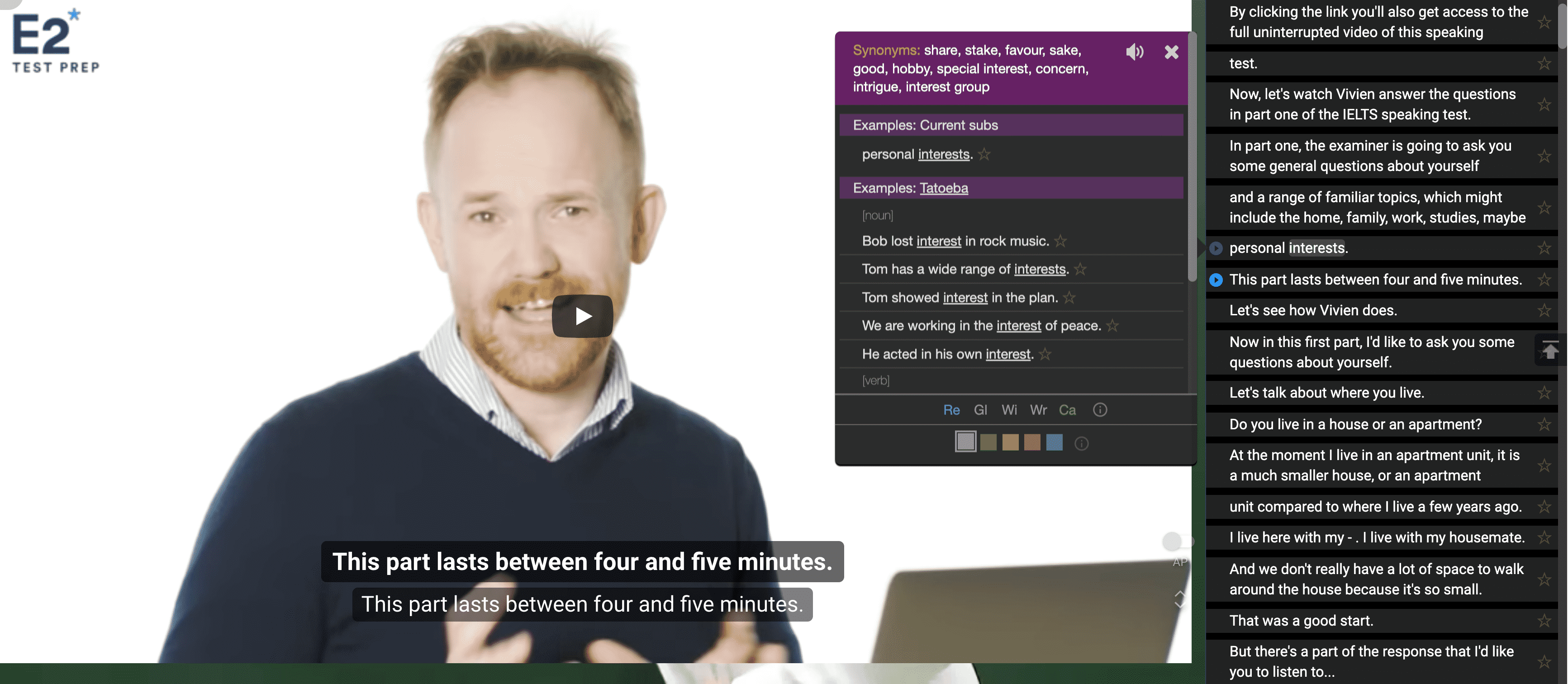
- [[YouGlish]] 是一个可以通过关键字来搜索发音的网站,非常适合用来学习单词或短语的发音
- [[Immersive Translate]] 是一款沉浸式的翻译插件,在浏览网页时可以将翻译内容附在原文下方。
- [[selectext]] 是一款可以复制视频内容的 Chrome 插件
Language Reactor
Language Reactor 是一个 Chrome 插件,可以在 Netflix,YouTube 等等流媒体平台上实时显示多语言字幕。
YouGlish
YouGlish 是一个通过单词短语来搜索视频(音频)的网站,非常适合用来学习英语发音,在网站中随便搜索一个单词,YouGlish 就会在 Youtube 上搜索包含这个单词的视频句子,听到真正的 Native Speaker 发音,可以通过模仿,重复来提高自己的英语口语。
也可以选择各种类型的发音,当然也可以学习其他语言。
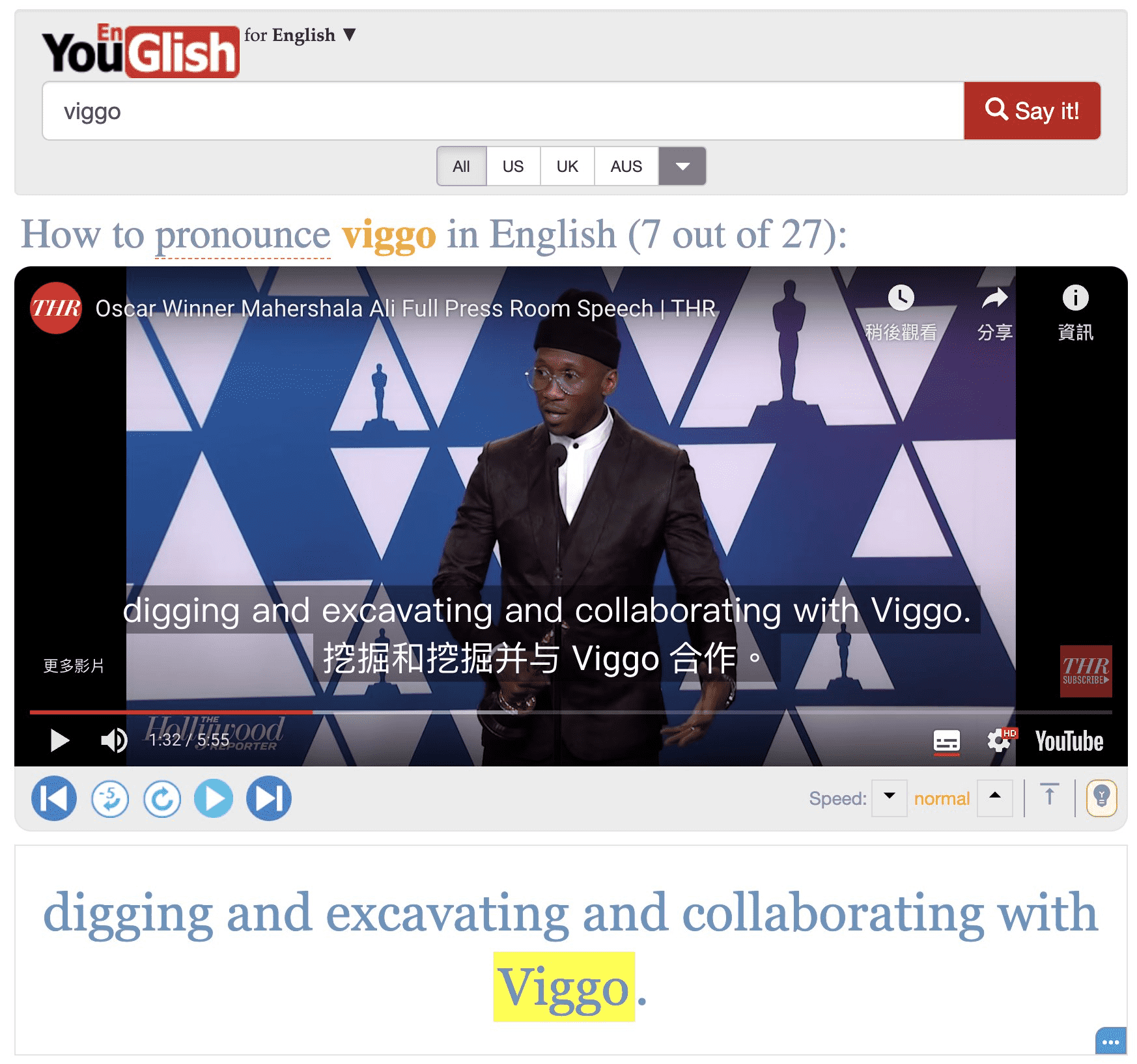
这个网站支持非常多的语言。
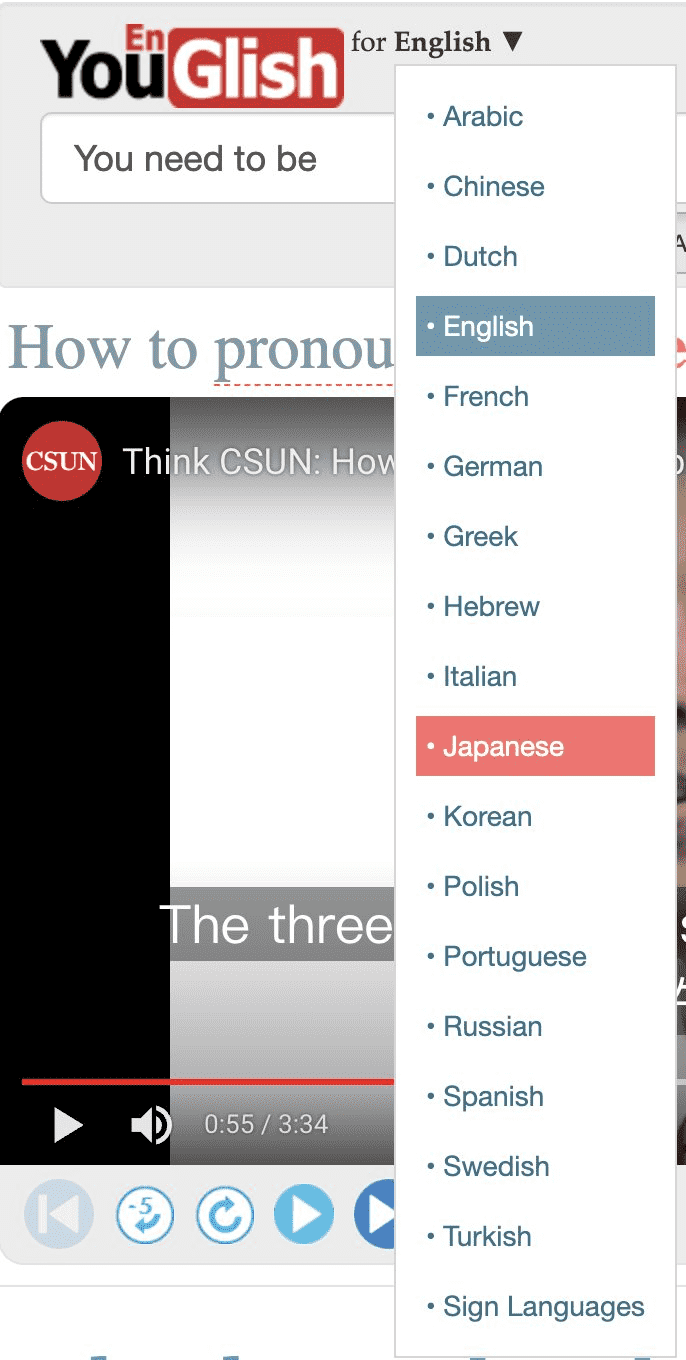
比如日语:
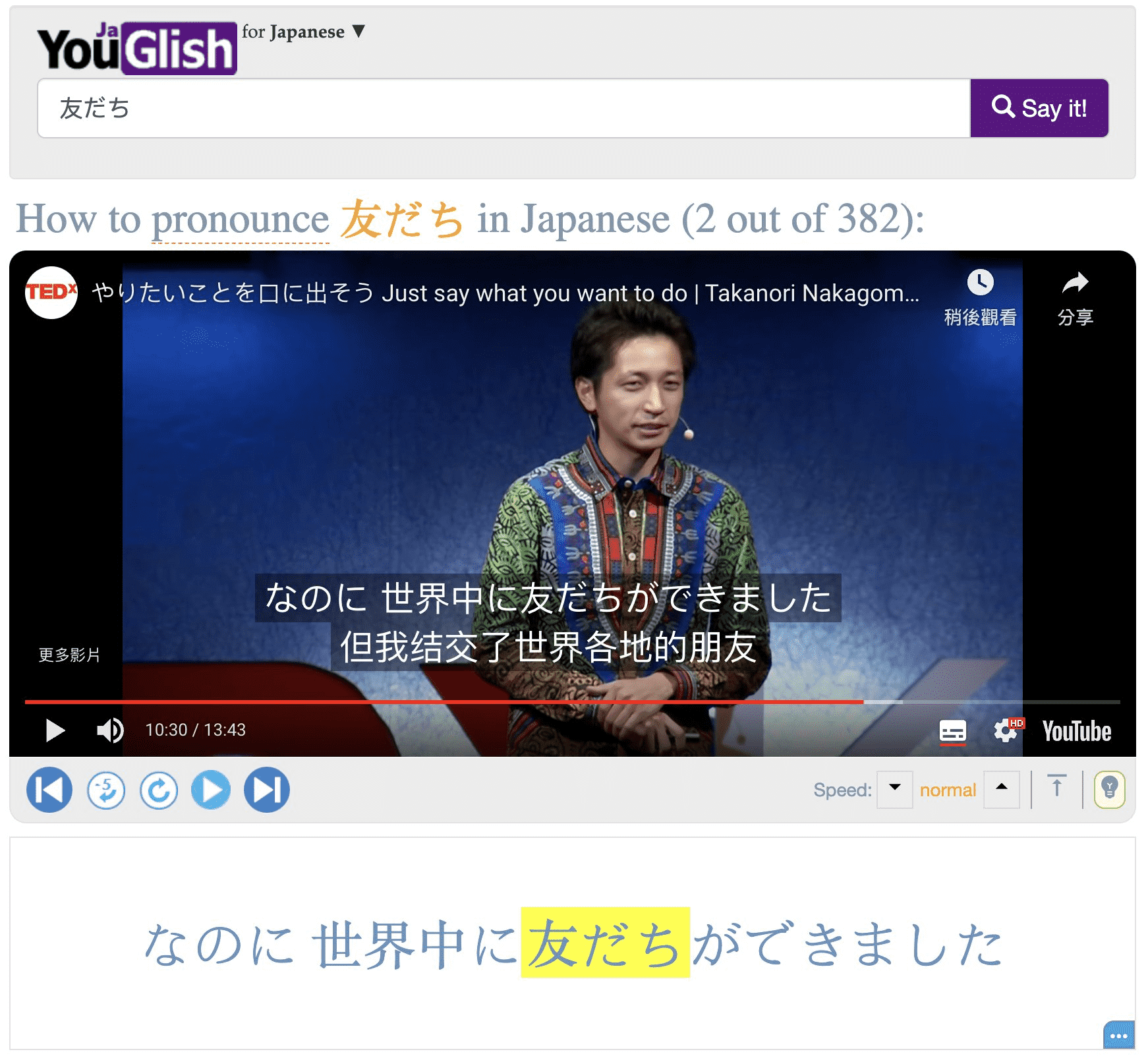
Immersive Translate
Immersive Translate 是一款开源的 Chrome 插件,可以将网页的内容翻译在原文下方。
比如当看到日文的,或英文的网页时,可以将翻译内容直接显示在文字下方。

selectext
selectext 是一款可以复制视频内文字的浏览器插件。当你在看英文,或其他语言教程的时候,遇到想要查字典的单词,可以暂停视频,然后复制视频中的文字。

比如当看到这个视频,想要查一下 町 的意思,就可以暂停视频,然后点击视频左上方的 S,之后插件就会对视频内容进行 OCR,视频出其中的文字,然后点击其中的方框就立即能复制到粘贴板中。
XML 数字签名及 Java 实现
数字签名是一种基于摘要算法和非对称加密技术的防止数据在传输过程中被篡改的安全技术。
数字签名的原理是对传输的内容做摘要(SHA245 等),然后把摘要和用到的摘要算法使用非对称加密技术的公钥或私钥(大部分情况下是私钥)生成签名。接收方接受到数据后,把签名信息用私钥或公钥验证来确保内容的完整性。
XML 数字签名
XML 数字签名是数字签名的基础上定义出来的一种 XML 数字签名规范,和普通的数字签名相比较有不少优点,比较灵活。XML 数字签名即可以对传输的所有内容签名,也可以只对传输的一小部分内容进行部分签名。不同的签名还可以使用不同的算法和密钥。[^1]
[^1]:https://www.w3.org/TR/xmldsig-core2/
XML Signature 是一个定义数字签名的 XML 语法的 W3C 推荐标准。从功能上或,XML Signature 与 PKCS#7 有很多共同点,但是 XML 签名具有更好的可扩展性,并为签名 XML 文档做了调整。XML Signature 在许多 Web 技术,如 SOAP, SAML 等中使用。
最近在调研日本 e-Gov 电子申请的时候,所使用的签名技术就是基于 XML 的签名,因为提交的数据格式是 XML ,并且涉及到敏感信息所以签名是必不可少的部分。
XML 数字签名的类型
XML 数字签名分成三种类型:
- Enveloped
- Enveloping
- Detached
它们的差别在于 XML 文档结构不同。
Enveloped
Enveloped 格式 XML 签名是把签名节点 Signature 直接嵌入到原始 XML 文档中。比如下方的样式中的 <Signature> 节点。
e-Gov 采用的方式就是这个 Enveloped 格式。
<?xml version="1.0" encoding="UTF-8"?>
<POrder>
<Item number="130055555232">
<Description>Game</Description>
<Price>19.99</Price>
</Item>
<Customer id="8492340">
<Name>My Name</Name>
<Address>
<Street>One Network Drive</Street>
<Town>Burlington</Town>
<State>MA</State>
<Country>United States</Country>
<PostalCode>01803</PostalCode>
</Address>
</Customer>
<Signature xmlns="http://www.w3.org/2000/09/xmldsig#">
<SignedInfo>
<CanonicalizationMethod
Algorithm="http://www.w3.org/TR/2001/REC-xml-c14n-20010315"/>
<SignatureMethod
Algorithm="http://www.w3.org/2000/09/xmldsig#rsa-sha1"/>
<Reference URI="">
<Transforms>
<Transform
Algorithm="http://www.w3.org/2000/09/xmldsig#enveloped-signature"/>
</Transforms>
<DigestMethod Algorithm="http://www.w3.org/2000/09/xmldsig#sha1"/>
<DigestValue>tVicG91o5+L31M=</DigestValue>
</Reference>
</SignedInfo>
<SignatureValue>
...
</SignatureValue>
<KeyInfo>
<X509Data>
<X509SubjectName>
CN=Your Name,O=Certificates Inc.,C=US
</X509SubjectName>
<X509Certificate>
...
</X509Certificate>
</X509Data>
</KeyInfo>
</Signature>
</POrder>
Enveloping
Enveloping 格式的 XML 签名和 Enveloped 正好相反,把原始 XML 文档作为子节点,插入到新生成的 Signature 节点的 Object 子节点中。
<?xml version="1.0" encoding="UTF-8"?>
<Signature xmlns="http://www.w3.org/2000/09/xmldsig#">
<SignedInfo>
<CanonicalizationMethod
Algorithm="http://www.w3.org/TR/2001/REC-xml-c14n-20010315"/>
<SignatureMethod
Algorithm="http://www.w3.org/2000/09/xmldsig#rsa-sha1"/>
<Reference URI="#order">
<DigestMethod Algorithm="http://www.w3.org/2000/09/xmldsig#sha1"/>
<DigestValue>+8cIU+LQ=</DigestValue>
</Reference>
</SignedInfo>
<SignatureValue>
...
</SignatureValue>
<KeyInfo>
<X509Data>
<X509SubjectName>
CN=Your Name,O=Test Certificates Inc.,C=US
</X509SubjectName>
<X509Certificate>
...
</X509Certificate>
</X509Data>
</KeyInfo>
<Object ID="order">
<POrder>
<Item number="130045555532">
<Description>Game</Description>
<Price>19.99</Price>
</Item>
<Customer id="849">
<Name>Your Name</Name>
<Address>
<Street>One Network Drive</Street>
<Town>Burlington</Town>
<State>MA</State>
<Country>United States</Country>
<PostalCode>01803</PostalCode>
</Address>
</Customer>
</POrder>
</Object>
</Signature>
这里需要注意的是 Reference 节点中指向的部分,如果使用空值表示指向文档根节点,而如果指定了值,那就是指向 XML 文档中的部分内容。
Detached
Detached 格式是指新生成的 Signature 节点作为一个独立的文档单独保存和传输,而不会对原始文档进行修改。
数字签名的应用场景
- 可靠信息交换
- 电子公文传输
XML 数字签名的结构
Signature 结构
对于 XML 签名来说就是根据 XML 文档内容以及证书生成下面的一个签名结构。
<Signature ID?>
<SignedInfo>
<CanonicalizationMethod />
<SignatureMethod />
(<Reference URI? >
(<Transforms>)?
<DigestMethod>
<DigestValue>
</Reference>)+
</SignedInfo>
<SignatureValue>
(<KeyInfo>)?
(<Object ID?>)*
</Signature>
举例
<署名情報>
<Signature
xmlns="http://www.w3.org/2000/09/xmldsig#" Id="20230720113000">
<SignedInfo>
<CanonicalizationMethod Algorithm="http://www.w3.org/TR/2001/REC-xml-c14n-20010315"></CanonicalizationMethod>
<SignatureMethod Algorithm="http://www.w3.org/2001/04/xmldsig-more#rsa-sha256"></SignatureMethod>
<Reference URI="#%E6%A7%8B%E6%88%90%E6%83%85%E5%A0%B1">
<Transforms>
<Transform Algorithm="http://www.w3.org/TR/2001/REC-xml-c14n-20010315"></Transform>
</Transforms>
<DigestMethod Algorithm="http://www.w3.org/2001/04/xmlenc#sha256"></DigestMethod>
<DigestValue>BdQwkfm3lyDWV2mTu+CxBPU=</DigestValue>
</Reference>
<Reference URI="900A01000200800001_01.xml">
<DigestMethod Algorithm="http://www.w3.org/2001/04/xmlenc#sha256"></DigestMethod>
<DigestValue>2WrlTW71oH+E6FuhxGR0=</DigestValue>
</Reference>
</SignedInfo>
<SignatureValue>gjeaEM7qng==</SignatureValue>
<KeyInfo>
<X509Data>
<X509Certificate>MIIEizCU</X509Certificate>
</X509Data>
</KeyInfo>
</Signature>
</署名情報>
Signature节点是数字签名根节点SignedInfo保存签名和摘要信息以及使用的各种算法SignedInfo中的CanonicalizationMethod子节点用来指定生成签名的 SignedInfo 节点规范化处理方法,具体的方法可以参考规范中的 「Exclusive XML Canonicalization」- 只有对 XML 内容规范化之后,才不会因为 XML 文档格式稍有不同而影响验证结果
SignatureMethod子节点用来指定签名使用的摘要算法和签名算法- 如果
Algorithm值是http://www.w3.org/2001/04/xmldsig-more#rsa-sha256表示使用的签名算法是 SHA256-RSA
- 如果
SignedInfo可以包含一个或多个Reference子节点,每个 Reference 用来指定某个引用的 XML 节点经过规范化后的摘要信息和生成摘要的方法- Reference 中会包含一个 URI 属性,用来指定对 XML 中哪一个节点进行签名,一般会是
#node,或者直接是指定文件名。 - Reference 中同样包含两个子节点,分别表示摘要的算法以及对指定内容进行摘要之后的值
- Reference 中会包含一个 URI 属性,用来指定对 XML 中哪一个节点进行签名,一般会是
SignatureValue用来记录整个SignedInfo节点经过规范化后输出内容的签名,并使用 Base64 编码算法转换成可见的字符串KeyInfo可选,用来保存验证签名的非对称加密算法公钥(只有公钥可以公开)Object节点是可选的,只有在 Enveloping XML 签名时才会用到
开发相关的库
- [[Apache Santuario]] 是 Apache 上一个 XML 安全性方面的项目,旨在实现对 XML 的主要安全标准。
XMLSec Library
XMLSec Library 支持 W3C 的 XML Signature 和 XML Encryption 规范,同时也支持 Canonical XML 和 Exclusive Canonical XML 规范。
XML 数字签名处理过程
主要工作是根据内容创建 Signature 节点。主要是分成三个步骤
- 第一步是根据指定的 XML 节点,生成 SignedInfo 中的 “Reference” 节点,Reference 节点会指定需要签名的对象,然后根据 Reference 指定的签名算法,生成签名值,比如在电子申请中,有两个 Reference,一个是
構成情報,另外一个是手续的申请书。 - 第二步是在 Reference 的基础上创建 SignedInfo 节点,并指定 SignedInfo 需要的规范化处理方法,以及签名算法
- 最后是根据 SignedInfo 以及证书,生成数字签名 SignatureValue,并最终生成完整的 Signature 节点
当有了完整的 Signature 节点之后再根据不同的格式对 XML 内容进行操作。
XML 签名验证
有 XML 签名的过程,同样在验证时只需要对上面的过程进行逆向就可以。当接收方接收到了包含 Signature 的 XML 文档。
- 首先根据 SignedInfo 中指定的规范化方法处理整个 SignedInfo 节点,保证不会因为格式问题出错,然后根据 SignatureMethod 中的数字签名算法验证签名信息,如果验证通过表示 SignedInfo 中的内容没有被篡改
- 然后开始验证 SignedInfo 中所有的 Reference 节点
- 通过定义的 URI 找到对应的 XML 节点,通常这个 XML 的 ID 应该是整个文档唯一的
- 根据 XML 中的节点,按照 Reference 中的 Transforms 指定的规范化方法处理
- 然后根据 DigestMethod 中指定的摘要算法对规范化之后的内容进行摘要处理
- 然后将摘要信息和 DigestValue 中的摘要值(Base64 解码)进行对比,一致则表示通过
通过以上的验证就可以确保传输的内容没有被篡改。
Java 实现
引入依赖
<dependency>
<groupId>org.apache.santuario</groupId>
<artifactId>xmlsec</artifactId>
<version>2.2.3</version>
</dependency>
编码例子
public static void sign(Key signKey, X509Certificate signCert, Element signElement) throws XKMSException {
String elementId = signElement.getAttribute("Id");
if (elementId == null) {
throw new XKMSException("Id of the signing element is not set");
}
String elementRefId = "#" + elementId;
IdResolver.registerElementById(signElement, elementId);
try {
XMLSignature signature = new XMLSignature(signElement
.getOwnerDocument(), elementRefId,
XMLSignature.ALGO_ID_SIGNATURE_RSA_SHA1,
Canonicalizer.ALGO_ID_C14N_EXCL_OMIT_COMMENTS);
signElement.appendChild(signature.getElement());
Transforms transforms = new Transforms(signElement
.getOwnerDocument());
transforms.addTransform(Transforms.TRANSFORM_ENVELOPED_SIGNATURE);
transforms
.addTransform(Transforms.TRANSFORM_C14N_EXCL_OMIT_COMMENTS);
signature.addDocument(elementRefId, transforms,
MessageDigestAlgorithm.ALGO_ID_DIGEST_SHA1);
signature.addKeyInfo(signCert);
signature.addKeyInfo(signCert.getPublicKey());
signature.sign(signKey);
} catch (XMLSecurityException xmse) {
throw new XKMSException(xmse);
}
}
reference
macOS 上的清理工具整理合集
最近 macOS 系统磁盘空间告急,之前就出现过因为磁盘空间不足导致系统卡顿还出现突然黑屏的状态,所以这次就看到还剩余几十个 GB 的时候就开始清理工作了。清理的同时顺便就整理一下常用的几个清理工具。
如何发现大文件
在清理之前首先要对本地磁盘文件做一个整体的了解,虽然 macOS 自带一个存储管理的查看面板,但是实在是太简陋,也只能提供非常简单地查找大文件的工具。
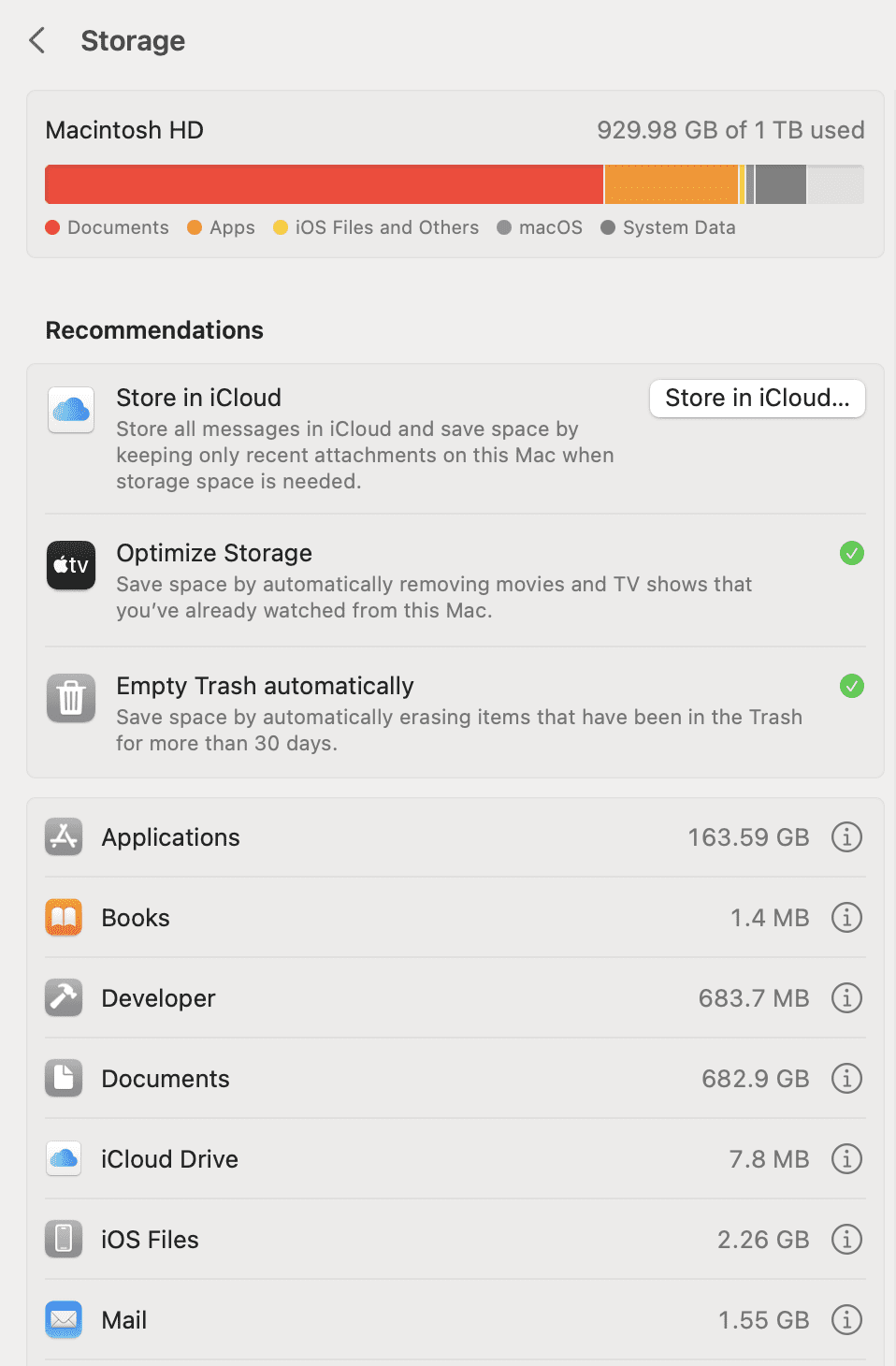
比如说从系统提供的 Storage 预览中能看到 Documents 占用的空间最多,可以点开后面的圆形 i 图标,可以看到其中占用空间很大的几个文件。
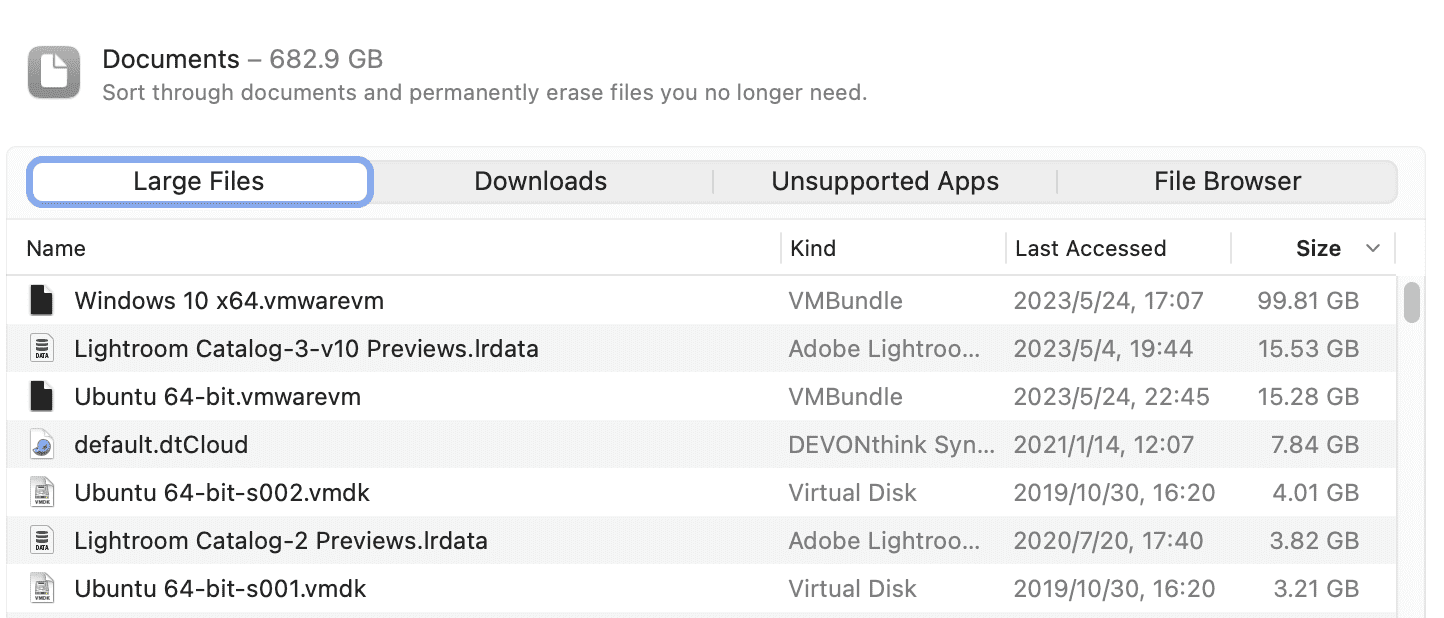
比如说对于我,就是我安装的两个虚拟机占用了比较多的空间,但这也是预想之内的。
gdu
上面的方式只能找出来系统中的大文件所在,如果我想知道每一个文件夹所占用的空间大小,我之前的文章中介绍过gdu ,这个时候就派上了用场。
brew install gdu
然后直接对想要统计的目录运行 sudo gdu ~/
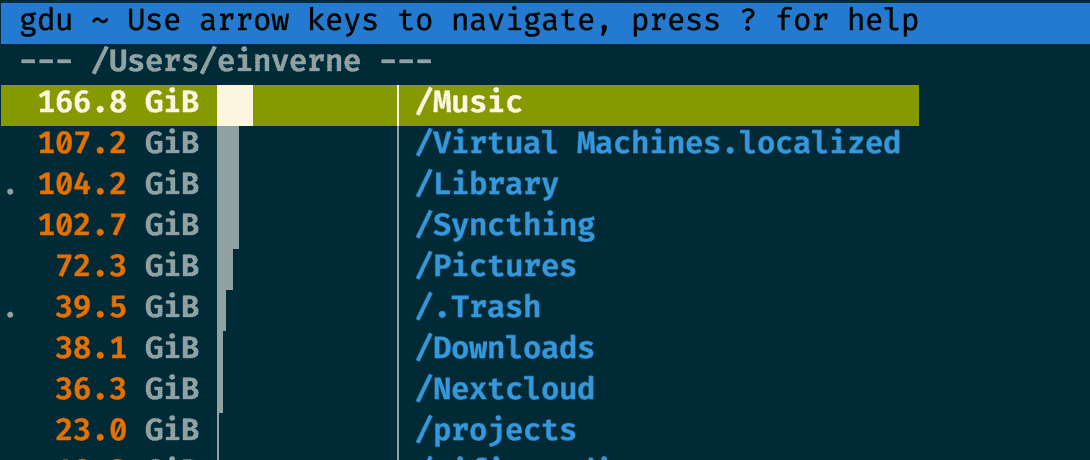
几款 macOS 上的清理工具
- [[Clean My Mac]] 收费软件
- [[Pretty Clean]] Pretty Clean 免费
- [[App Cleaner]] 免费,卸载应用
- [[Clean Me]] Clean Me 是一款开源的清理磁盘工具
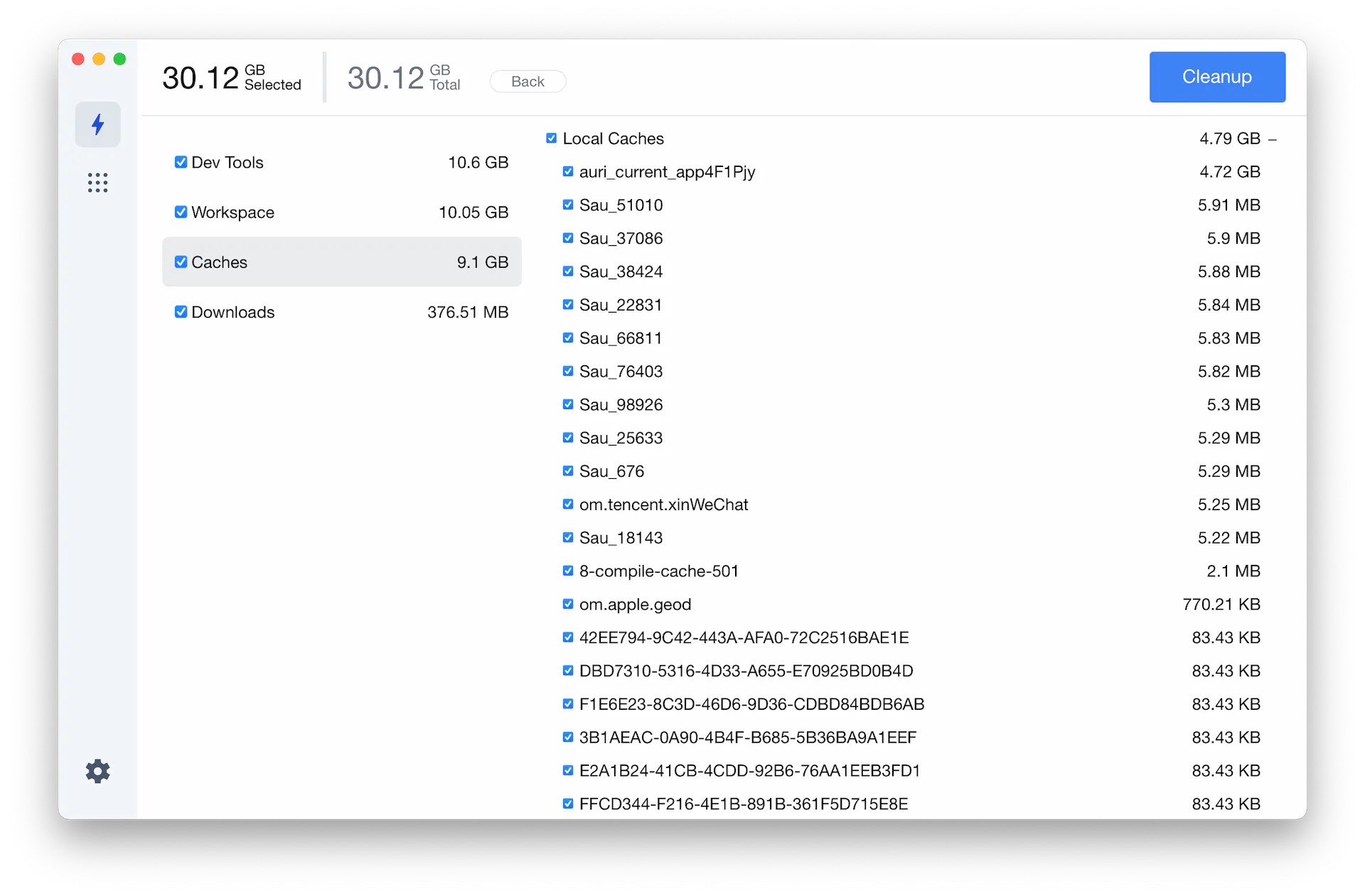
Pretty Clean
PrettyClean 是一款 macOS 上的免费清理工具,界面非常简单。
App Cleaner
App Cleaner 是一款可以用来快速卸载应用以及应用相关残留文件的应用,非常小巧,但是非常强大。
脚本
- mac-cleanup-py 是一个 macOS 上的清理脚本。
使用 Listmonk 搭建自己的 Newsletter
listmonk 是一个开源的,使用 Go 语言编写的,自托管的邮件列表订阅应用。目前已经在 GitHub 收获了超过 10000 颗星星,listmon 速度非常快,功能丰富,并且可以直接打包成一个二进制文件,和 PostgreSQL 数据库一起使用。
借助 listmonk 可以非常快速的搭建属于自己的 Newsletter,Newsletter 是一种基于邮件的时事通讯,企业或组织可以通过邮箱给其成员,客户,员工或其他订阅者发送活动的新闻及广告营销的方式,但最近也逐渐成为个人出版、自媒体的流行订阅形式,相比 RSS,它更加自主,有更好的阅读体验,并且可以有更灵活的付费方式。
特性:
- 支持公共列表和私有列表
- 只依赖 [[PostgreSQL]]
- 拥有管理面板
- 基于 Go 的模板、支持 WYSIWYG 编辑器
- 多线程,多 SMTP 邮件队列,用于快速投递邮件
- HTTP,JSON API
- 点击和视图追踪
- 支持导入 [[MailChimp]] 和 [[Substack]] 的订阅用户
安装
具体的 docker-compose 可以看这里,listmonk 需要依赖一个配置文件,我一般习惯直接放在 HOME 目录中
git clone git@github.com:einverne/dockerfile.git
cd dockerfile/listmonk
cp env .env
# edit .env
# create config.toml
vi ~/listmonk/config.toml
然后填入一下内容。注意将配置文件中的内容填写,比如用户名和密码,数据库连接方式替换为自己的内容。
[app]
# Interface and port where the app will run its webserver.
address = "0.0.0.0:9000"
admin_username = "username"
admin_password = "password"
# Database.
[db]
host = "host"
port = 5432
user = "listmonk"
password = "pass"
database = "listmonk"
ssl_mode = "disable"
max_open = 25
max_idle = 25
max_lifetime = "300s"
当添加完配置文件之后,就可以使用 docker-compose up -d db 来启动数据库了,但是 listmonk 应用不回初始化数据库 Schema,所以还需要进行初始化数据库操作。
docker-compose run --rm app ./listmonk --install
等初始化数据操作完成,可以通过进入 PostgreSQL 容器查看表结构来验证。
docker exec -it listmonk_db /bin/bash
psql -d listmonk -U listmonk -W
\dt
最后就可以启动应用 docker-compose up -d
自定义静态模板文件
这部分内容已经在我上面提及的 docker-compose.yml 文件中存在。
app:
<<: *app-defaults
container_name: listmonk_app
depends_on:
- db
command: "./listmonk --static-dir=/listmonk/static"
volumes:
- "${LISTMONK_CONFIG}/config.toml:/listmonk/config.toml"
- "./static:/listmonk/static"
导入外部订阅用户
加入已经在 [[MailChimp]] 或者 [[Substack]] 上有一定的订阅用户,那么可以通过后台工具导入 csv 文件。但需要注意的是,导入的用户默认状态是 Unconfirmed,所以需要进入数据库手动更新用户的状态。
docker exec -it listmonk_db /bin/bash
psql -d listmonk -U listmonk -W
输入密码登录数据库,然后执行 \dt 查看表。然后查看表内容
SELECT * from subscriber_lists;
然后更新所有人
UPDATE subscriber_lists SET status='confirmed' WHERE list_id=4;
设置 SSL
默认情况下 listmonk 运行在 HTTP,不提供 SSL,我们可以借助 Nginx 和 Let’s Encrypt 来生成证书提供更安全的访问。
有很多种方式可以完成
- 在服务器上安装 Nginx,然后使用 certbot 生成 SSL 证书并自动续期
- 也可以利用 Nginx Proxy Manager 来管理 Docker 中的服务,自动暴露 Docker 端口,然后提供 SSL 访问
- 或者如果不想有一个 Web UI 管理界面,也可以利用 Nginx Proxy 自动管理 Docker 中的服务,生成证书
- 在这边因为我已经安装了 HestiaCP 控制面板 就直接借助其自带的 Nginx
之前好几篇文章也介绍过 HestiaCP 面板中的模板文件,所以这里就简单再总结一下。
首先与进入 root 账户 sudo su -
然后进入如下的目录
cd /usr/local/hestia/data/templates/web/nginx/php-fpm/
这个目录中包含了 HestiaCP 默认的 Nginx 模板。
cp default.tpl listmonk.tpl
cp default.stpl listmonk.stpl
然后分别修改这两个新生成的 listmonk 配置文件。
将其中 location 部分修改
location / {
proxy_pass http://localhost:9001;
proxy_set_header Host $http_host;
proxy_set_header X-Real-IP $remote_addr;
proxy_set_header X-Forwarded-For $proxy_add_x_forwarded_for;
}
然后最好把 stpl 文件中的 proxy_hide_header Upgrade; 删除。
再进入 HestiaCP 管理后台,创建用户,然后创建网站,填入域名。创建域名进入高级管理,在 Web Template(Nginx)中选择刚刚创建的 listmonk,保存。然后在高级设置中,配置 SSL,等待获取证书,保存之后就能通过域名来访问 listmonk 了。
Upgrade
如果使用 Docker 安装,那么升级非常简单,更新镜像,更新数据库,重启即可。
docker compose pull
docker compose run --rm app ./listmonk --upgrade
docker compose up app db
related
- [[SendPortal]]
- [[Mautic]]
文章分类
最近文章
- AI Shell 让 AI 在命令行下提供 Shell 命令 AI Shell 是一款在命令行下的 AI 自动补全工具,当你想要实现一个功能,敲一大段命令又记不住的时候,使用自然语言让 AI 给你生成一个可执行的命令,然后确认之后执行。
- 最棒的 Navidrome 音乐客户端 Sonixd(Feishin) Sonixd 是一款跨平台的音乐播放器,可以使用 [[Subsonic API]],兼容 Jellyfin,[[Navidrome]],Airsonic,Airsonic-Advanced,Gonic,Astiga 等等服务端。 Sonixd 是一款跨平台的音乐播放器,可以使用 [[Subsonic API]],兼容 Jellyfin,[[Navidrome]],Airsonic,Airsonic-Advanced,Gonic,Astiga 等等服务端。
- 中心化加密货币交易所 Gate 注册以及认证 Gate.io 是一个中心化的加密货币交易所。Gate 中文通常被称为「芝麻开门」,Gate 创立于 2013 年,前身是比特儿,是一家致力于安全、稳定的数字货币交易所,支持超过 1600 种数字货币的交易,提供超过 2700 个交易对。
- 不重启的情况下重新加载 rTorrent 配置文件 因为我在 Screen 下使用 rTorrent,最近经常调试修改 rtorrent.rc 配置文件,所以想要找一个方法可以在不重启 rTorrent 的情况重新加载配置文件,网上调查了一下之后发现原来挺简单的。
- Go 语言编写的网络穿透工具 chisel chisel 是一个在 HTTP 协议上的 TCP/UDP 隧道,使用 Go 语言编写,10.9 K 星星。